扇形の弧の長さと面積

扇型（Circular Sector）

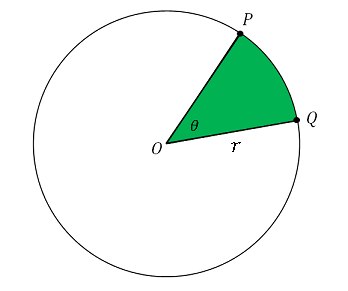
円の中心 $O$ から円周上の $2$ 点 $P,Q$ に引いた $2$ 本の線分 $OP,OQ$ と、円弧 $PQ$ に囲まれた図形を 扇形（circular sector）とよびます。$2$ 本の線分 $OP,OQ$ の間の角 $\mathrm{\angle }POQ$ を 扇形の中心角 といいます。

扇形の弧（円弧）の長さ

下図のように、半径が $r$、角度が $\theta$ の扇形を考えます。



扇形の弧長（円弧の長さ）$l$ は中心角 $\theta$ に比例します。
この扇形と同じ半径をもつ円周の長さは $L=2\pi r$ なので、
$$l=2\pi r\frac{\theta }{{360}^{\circ }}$$
となります。角度を 弧度法 で表すと、
$$l=2\pi r\frac{\theta }{2\pi }=r\theta$$
という式で表されます。

扇形の面積

下図のように、半径 $r$、角度 $\theta$ の扇形を考えます。



扇形の面積 $S$ は中心角 $\theta$ に比例します。
この扇形と同じ半径をもつ円の面積は $S=\pi r^2$ なので、
$$S=\pi r^2\frac{\theta }{{360}^{\circ }}$$
となります。角度を 弧度法 で表すと、
$$l=\pi r^2\frac{\theta }{2\pi }=\frac{1}{2}{r}^2\theta$$
となります。

【解答】扇形の弧長は
$$l=2\pi \times 4\times \frac{{60}^{\circ }}{{360}^{\circ }}=\frac{4\pi }{3}$$
扇形の面積は
$$S=\pi \times 4^2\times \frac{{60}^{\circ }}{{360}^{\circ }}=\frac{8\pi }{3}$$
となります。

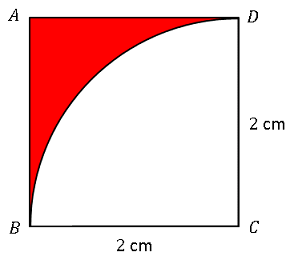[例題 02] 一辺が $2\mathrm{cm}$ の正方形があります。図のように、この正方形の一辺と同じ長さの半径をもつ扇形によって正方形を切り取ります。この切り取られた赤い部分の面積を求めてください。

【解答】赤い部分の面積を $S$ とします。正方形から扇形の面積を引けばよいので、
$$S=4-\frac{4\pi }{4}=(4-\pi ){\mathrm{cm}}^2$$
となります。