ペアノの公理

数学は 自然数 (natural number)
\[1,\:2,\:3,\:4,\:5,\:6,\:7,\:8,\:9,\:\cdots\]
を定義することから始まります。自然数の集合を $\mathbb{N}$ と表記し、ある数 $a$ が自然数に属することを $a\in\mathbb{N}$ と表します。

ペアノの公理（Peano axioms）

自然数の厳密な定義はペアノの公理 (Peano axioms)によって与えられます。

[1] 自然数 $1$ が存在する。
[2] 任意の自然数 $a$ には、後継 $\mathrm{suc}(a)=a+1$ が存在する。
[3] $1$ はいかなる自然数の後継 (successor) でもない。
[4] $a\neq b$ ならば、$\mathrm{suc}(a)\neq\mathrm{suc}(b)$
[5] $1$ がある性質 $P$ を満たすという条件のもとで、$a$ が $P$ を満たせば後継 $a+1$ も $P$ を満たすとき、すべての自然数は $P$ を満たす。

[1] によって数学における単位（あるいは要素）がまず１つ定められます。
[2] によって、$1$ から作られる数字の列
\[1,\quad\mathrm{suc}(1),\quad\mathrm{suc}(\mathrm{suc}(1)),\quad\cdots\]
が無限に定義されます。$a+1$ の記号で書けば
\[1,\quad 1+1,\quad 1+1+1,\quad\cdots\]
となります。これらにアラビア数字を当てはめて、
\[\begin{align*}&1=1\\[6pt]&1+1=2\\[6pt]&1+1+1=3\end{align*}\]
というように定めます。もちろん当てはめるものは漢数字でもアルファベットでも構いません。$1+1+1$ という記法のままでも数学はできるかもしれませんが、とても煩わしいので、すぐに嫌になってしまうでしょう。

[3] は $1$ が最初の数であることを示しています。自然数に $0$ を含める定義の仕方もありますが、当サイトでは基本的に $1$ から始まる数字を自然数と定義します。扱う分野によって $0$ を含める必要があるときはその旨を明記します。

[4] は１つの数に唯１つの後継を対応させるということです。
いわゆる「全単射」とよばれる写像です。対偶をって「$\mathrm{suc}(a)=\mathrm{suc}(b)$　ならば　$a=b$」と言い換えることもできます。もし仮にこの定義がなければ、たとえば下図のように、$a$ の後継 $a+1$ が $a$ とは異なる数字 $b$ の後継にもなって、循環を生じてしまう可能性もあります。



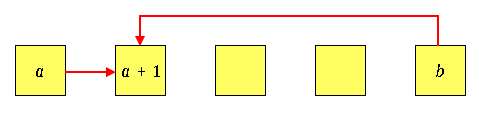
すなわち [4] によって、自然数は整然と順番に並ぶことになります。

[5] は、よく知られた数学的帰納法の原理です。
詳しくはこちらの記事を参照してください。

自然数の加算（足し算）

自然数 $a$ と $b+1$ の加算というものを次のように定義します。
\[a+\mathrm{suc}(b)=\mathrm{suc}(a+b)\]
$\mathrm{suc}(n)$ を $n+1$ で表すと
\[a+(b+1)=(a+b)+1\]
たとえば $5$ と $3$ を加える場合、$3=2+1$ なので
\[\begin{align*}&5+1=6\\[6pt]&5+2=5+(1+1)=(5+1)+1=6+1=7\\[6pt]&5+3=5+(2+1)=(5+2)+1=7+1=8\\[6pt]\end{align*}\]
というように再帰的に計算できます。つまり $5$ から数えて $3$ 番目の後継が答えとなります。原初の記法
\[5=1+1+1+1+1,\quad 3=1+1+1\]
を用いると
\[\begin{align*}5+3\,&=(1+1+1+1+1)+(1+1+1)\\[6pt]&=1+1+1+1+1+1+1+1=8\end{align*}\]
となります。

自然数の乗算（掛け算）

自然数の乗算は次のように定義されます。
\[\begin{align*}&a\times 1=1\\[6pt]&a\times (b+1)=(a\times b) +a\end{align*}\]
たとえば $7\times 3$ は次のように計算できます。
\[\begin{align*}&7\times 1=7\\[6pt]&7\times 2=7\times (1+1)=(7\times 1)+7=7+7=14\\[6pt]&7\times 3=7\times (2+1)=(7\times 2)+7=14+7=21\\[6pt]\end{align*}\]

結合／交換／分配法則

自然数の加算と乗算は次の結合／交換／分配法則を満たします。
\[\begin{align*}&(a+b)+c=a+(b+c)\\[6pt]&a+b=b+a\\[6pt]&(a\times b)\times c=a\times(b\times c)\\[6pt]&a\times b=b\times a\\[6pt]&a\times (b+c)=(a\times b)+(a\times c)\end{align*}\]
いずれもペアノの公理から簡単に導くことができます。

自然数の減算（引き算）

$a$ に加えて $b$ となるような $x$, すなわち
\[a+x=b\]
を満たすような $x$ を求めることを減算 (引き算) とよび、
\[x=b-a\]
と表します。ここに「$-$」はマイナス記号と呼ばれる演算子であり、$b-a$ を「$b$ 引く $a$」とか「$b$ マイナス $a$」と読みます。たとえば、
\[20+30=50\]
という加算が成り立っているので、
\[30=50-20\]
となります。しかし、
\[10-10\]
のような計算は自然数の範囲では不可能です。
\[10+x=10\]
を満たす $x$ は $\mathbb{N}$ に存在しないからです。このような演算を成立させるには、上の式を満たすような要素 $x$ を集合に含めるしかありません。同じように
\[5-10\]
というような引き算もできません。やはり
\[10+x=5\]
となるような要素 $x$ がないからです。

自然数の除算（割り算）

自然数 $a,\:b$ に対して、除算（割り算）は
\[a=bq+r \quad(r\lt b)\]
によって定義されます。ここに $q$ が除算の結果（商）であり、$r$ は剰余（余り）とよばれます。たとえば $17$ を $3$ で割ると、
\[17=3\times 5+2\]
なので、商は $5$, 余りは $2$ となります。この演算を「$\div$」という記号を用いて
\[17\div 3=5\:\cdots\:2 \]
のように表すこともあります。