命題の真偽・否定・逆・裏・対偶

$p$ という仮定（assumption）に対して $q$ という結論（conclusion）が真 (true) であるのか偽 (false) であるのかの２択で定まるような文章や数式のことを命題（proposition） とよび、「$p\;\Longrightarrow\;q$」 のように表します ($p$ ならば $q$ と読みます)。

たとえば実数 $x$ について
\[x=2\:\Longrightarrow\;x^2=4\]
は成立するので、この命題は真です。

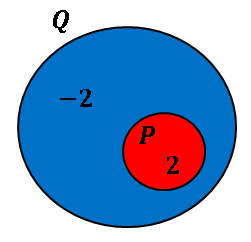
$p$ をみたす要素の集合を $P$, $q$ をみたす要素の集合を $Q$ とすると、命題が真であるときは $P$ の要素はすべて $Q$ に含まれます ($P\subset Q$)。先ほどの命題
\[x=2\;\Longrightarrow\;x^2=4\]
では、集合 $P$ と $Q$ の要素はそれぞれ
\[\begin{align*}&P=\{x\mid x=2\}\\[6pt]
&Q=\{x\mid x=-2,\:2\}\end{align*}\]
となるので、ベン図を書くと次のようになります。

否定（Negation）

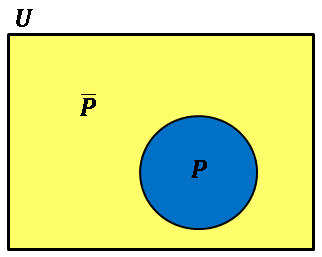
条件 $p$ に対して「$p$ ではない」ことを $p$ の否定 (negation) とよび、$\bar{p}$ または $\lnot{p}$ と書きます。$p$ をみたす要素の集合を $P$ とすると、$\bar{p}$ をみたす要素の集合は $P$ の補集合 $\bar{P}$となります。



先ほどの命題
\[x=2\;\Longrightarrow\;x^2=4\]
においては、$p$ の否定 $\bar{p}$ は $x\neq 2$ であり、$\bar{p}$ をみたす集合 $\bar{P}$ の要素は $x=2$ を除くすべての実数ということになります。

全称記号と存在記号

数学の命題でよく用いられるのが「任意の（すべての）」、「ある（存在する）」という言い回しです。英語ではそれぞれ all, some で表現します。数学では「任意の」を全称記号 $\forall$ で表すことがあります。これは All の A をひっくり返したものです。たとえば「すべての実数 $x$ に対して $x^2\geq 0$ が成り立つ」という命題を
\[\forall x \in\mathbb{R},\:x^2\geq 0\]
のように表せます。また「ある」は存在記号 $\exists$ を用います。こちらは Exist の E を逆さまにしたものです。たとえば「ある実数 $x$ が存在して、$x\lt 1$ をみたす」という命題は
\[\exists x \in\mathbb{R},\:x\lt 1\]
と書くことができます。「任意の」の否定は「ある」、「ある」の否定は「任意の」です。否定なので命題の真偽は引っくり返ります。たとえば「すべての実数 $x$ に対して $x^2\geq 0$ が成り立つ」という命題は真ですが、この命題を否定して「ある実数 $x$ が存在して、$x^2\lt 0$ が成り立つ」という命題にすると、$x^2\lt 0$ をみたすような実数 $x$ は存在しないので偽となります。記号で表すと
\[\exists x \in\mathbb{R},\:x^2\lt 0\]
となります。

命題の逆（Converse）

ある命題「$p\;\Longrightarrow\;q$」に対して
\[q\;\Longrightarrow\;p\]
を命題の逆（converse） といいます。もとの命題が真であっても、その逆も真であるとは限りません。たとえば実数 $x$ についての命題
\[x=2\;\Longrightarrow\;x^2=4\]
は真ですが、その逆命題
\[x^2=4\;\Longrightarrow\;x=2\]
については、$x^2=4$ をみたす実数 $x$ は $x=-2,\:2$ という２通りあるので、こちらは偽となります。

命題の裏（Inverse）

ある命題「$p\;\Longrightarrow\;q$」に対して
\[\bar{p}\;\Longrightarrow\;\bar{q}\]
を命題の裏（inverse）といいます。もとの命題が真であっても、その裏も真であるとは限りません。たとえば実数 $x$ についての命題
\[x=2\;\Longrightarrow\;x^2=4\]
は真ですが、その裏命題
\[x\neq 2\;\Longrightarrow\;x^2\neq 4\]
については、$x=-2$ もまた $x^2=4$ となるので、こちらは偽となります。

命題の対偶（Contraposition）

ある命題「$p\;\Longrightarrow\;q$」に対して
\[\bar{p}\;\Longrightarrow\;\bar{q}\]
を命題の対偶（contraposition）といいます。もとの命題の真偽と対偶の真偽は必ず一致します。この事実はベン図を用いるとすぐに理解することができます。$p\;\Longrightarrow\;q$ をみたす状況は次のようになります。



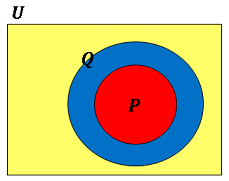
この図から $\bar{Q}$ と $\bar{P}$ を取り出して描いてみると下図のようになります。



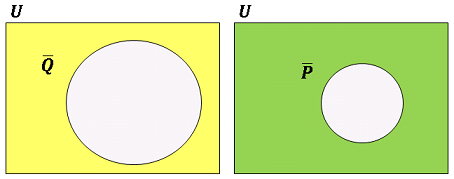
$\bar{Q}\subset \bar{P}$ という包括関係があることがわかります。もとの命題と対偶の真偽は必ず一致するので、ある命題が証明しにくいと思ったら、その対偶をとって証明を試みると上手くいくことがあります。

命題の逆・裏・対偶の関係図

命題の逆・裏・対偶の関係をまとめると下の図のようになります。



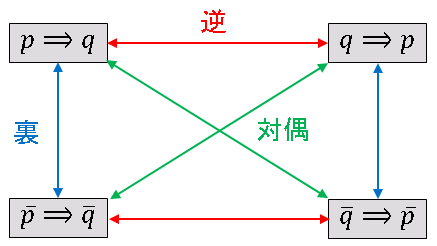
逆と裏については、もとの命題と真偽が一致するとは限らず、対偶のみがもとの命題と同値であることに注意してください。