変数分離型微分方程式の解法

変数分離型

次のような微分方程式
 \[\frac{dy}{dx}=X(x)Y(y)\tag{A}\]
を考えます。右辺が $x$ の関数 $X(x)$と $y$ の関数 $Y(y)$ の積となっています。このような形の微分方程式を 変数分離型 といいます。ただし $y$ は $x$ の関数 $y(x)$ なので、$Y(y)$ は $y$ を介して $x$ の関数となっています。両辺を $Y(y)$ で割ると、
 \[\frac{1}{Y(y)}\frac{dy}{dx}=X(x)\tag{A-1}\]
となります。両辺を積分すると
 \[\int\frac{1}{Y(y)}\frac{dy}{dx}dx=\int X(x)dx\tag{A-2}\]
となりますが、ここで置換積分の公式
 \[\int f(x)dx=\int f(x)\frac{dx}{dt}dt\]
と用いると左辺は
 \[\int\frac{1}{Y(y)}\frac{dy}{dx}dx=\int\frac{1}{Y(y)}dy\]
と書けるので、式 (A-2) は
 \[\int\frac{1}{Y(y)}dy=\int X(x)dx+c\tag{A-3}\]
となります ($C$ は積分定数) 。これは形式的にもとの微分方程式 (A) の両辺に $dx$ をかけるという操作をしてもかまわないことを示しています。したがって、今後は (A) のような微分方程式はいきなり
 \[\frac{dy}{Y(y)}=X(x)dx\tag{A-4}\]
というように変形してから両辺を積分します。上式の左辺は $y$ の関数とその変化量 $dy$ , 右辺は $x$ の関数とその変化量 $dx$ のみで表されています。このような式変形を変数分離とよびます。

【変数分離型方程式の例①】最も基本的な変数分離型方程式
 \[\frac{dy}{dx}=ky\tag{B}\]
を解いてみます。式 (A) において $X(x)=k,\:Y(y)=y$ とした方程式です。変数分離すると
 \[\frac{dy}{y}=kdx\]
となります。両辺を積分すると
 \[\begin{align*}\int\frac{dy}{y}=\int kdx\\[6pt]\log\mid y\mid=kx+c\\[6pt]\mid y\mid=e^ce^{kx}\\[6pt]y=\pm e^ce^{kx}\end{align*}\]
という解が得られます。ここで $y=0$ も (B) の解となっていますが、$\pm e^c \neq 0$ なので、そのままでは上の解に含まれません。しかし $A$ を 0 も含めた任意の定数として
 \[y=Ae^{kx}\]
とすれば、(B) の全ての解を含むことになります。

【変数分離型方程式の例②】次は右辺に $y^2$ を含む形の
 \[\frac{dy}{dx}=1-y^2\tag{C}\]
を解いてみます。変数分離すると
 \[\frac{dy}{y^2-1}=-dx\]
両辺を積分すると右辺は $-x+c$ となり、左辺は
 \[\int[\frac{dy}{y^2-1}=\frac{1}{2}\int\left[ \frac{1}{y-1}-\frac{1}{y+1}\right]=\frac{1}{2}\log\,\left| \frac{y-1}{y+1}\right|\]
となるので、
 \[\log\,\left| \frac{y-1}{y+1}\right|=-2x+c\tag{C-1}\]
$A=\pm e^c$ とおけば、
 \[y=\frac{1+Ae^{-2x}}{1-Ae^{2x}}\tag{C-2}\]
という解が得られます。また $1-y^2=0$ より $y=\pm 1$ という特解もありますが、これは上の式で $A=0$ または $A=\pm \infty$ とおいたものに等しくなっているので、改めて $A$ を任意の定数とすれば、上の解は全ての解を含むことになります。この微分方程式の解曲線を Excel でプロットすると下図のようになりした。
 

 
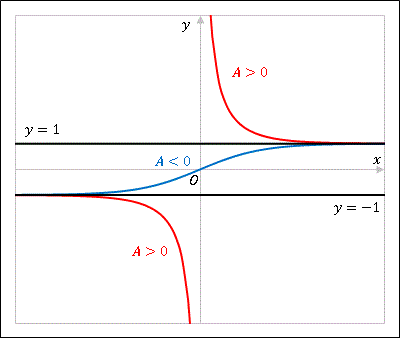
上図を見ると、解曲線群は $y=\pm 1$ を境に分離されています。