x の x 乗根のグラフを描きます

$y=\sqrt[x]{x}$

　$x$ の $x$ 乗根というちょっと変わった関数を調べてみましょう：
　
\[y=\sqrt[x]{x}\quad (x \gt 0) \tag{1}\]
　まずは理屈抜きに Excel で関数のグラフを描いてみます。

　
　
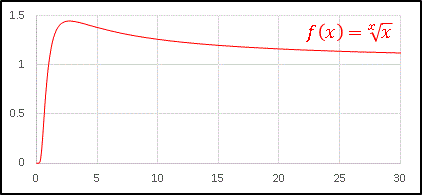
　急激に立ち上がって極大値をとったあとにゆっくりと減少していますね。
　この関数の極大値を求めてみましょう。(1) の両辺の対数をとると
　
\[\log y=\frac{\log x}{x}\]
となるので両辺を微分すると
　
\[\frac{y’}{y}=\frac{1-\log x}{x^2}\]
　$y$ は常に正ですから、$y=0$ となるのは $x=e$ です。
　このとき $y$ は極大値 $\sqrt[e]{e}$ をとります。
　あと原点付近に妙なところがありますね。少し拡大してみましょう。

　
　
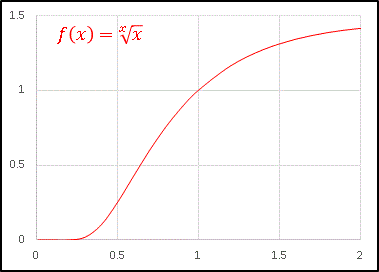
　$x$ が非常に小さい値をとる間は $x$ 軸にべったりと貼りついたようになっていますね。ところでこの関数は $x\rightarrow \infty$ で 1 に収束するのですが、その速度は非常に遅く、 $y=1.05$ に達するのは $x=92$ のときで、また $y=1.01$ となるのは $x=620$ のときです。 $x$ が大きくなる程度と、$x$ 乗根による抑え込みが非常に拮抗しているということです。

$y=\sqrt[x]{x} \cos x$

　三角関数を掛けてみましょう。

　
　
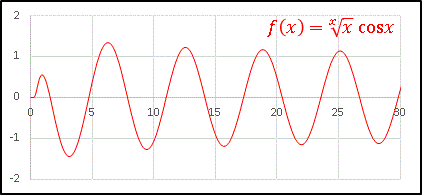
　減衰振動関数ですが、 $\sqrt[x]{x}$ の収束が遅いので振幅の減衰はとてもゆっくりです。

$y=\sqrt[x]{x} \log x$

　今度は対数関数を掛けてみます。

　
　
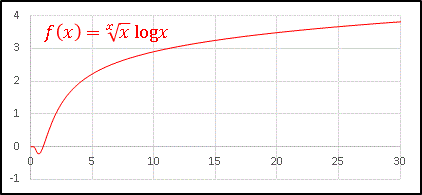
　全体的には増加関数ですが、また原点付近に気になるところがあります。
　拡大してみましょう。

　
　
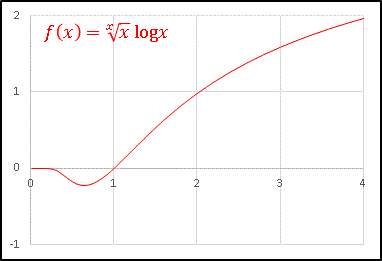
　$x=0.6$ あたりで小さな極小値をとっていますね。
　対数関数の負の値が寄与しているからです。　≫ Excel 数学グラフ