【Excel】連立方程式の数値解

この記事ではExcel関数を使って、連立方程式の数値解を求める方法について解説します。

【Excel】連立方程式の数値解

準備として、連立方程式を行列で解く方法について、簡単に説明しておきます。次のような連立方程式を考えます。
 \[\begin{align*}ax+by=p\\[6pt]cx+dy=q\end{align*}\]
ここで行列 $A$ とベクトル $\boldsymbol{x},\:\boldsymbol{b}$ を
 \[A=\begin{pmatrix}a & b\\ c & d\end{pmatrix},\:\boldsymbol{x}=\binom{x}{y},\ \boldsymbol{b}=\binom{p}{q}\]
とおくと、連立方程式は
 \[A\boldsymbol{x}=\boldsymbol{b}\]
と表せます。両辺に逆行列を左からかけます。
 \[A^{-1}A\boldsymbol{x}=A^{-1}\boldsymbol{b}\]
$A^{-1}A=I$ ($I$ は単位行列) なので、
 \[I\boldsymbol{x}=A^{-1}\boldsymbol{b}\]
さらに、$I\boldsymbol{x}=\boldsymbol{x}$ なので、
 \[\boldsymbol{x}=A^{-1}\boldsymbol{b}\]
となります。逆行列を用いると、このように解ベクトル $\boldsymbol{x}$ を機械的に計算できますが、$\det{A}=ad-bc=0$ のときは逆行列は存在せず、方程式も解をもたなかったり不定であったりします。

それでは、Excel を使って連立方程式の数値解を求めてみましょう。下図を参照にシートを作っていきます。
 

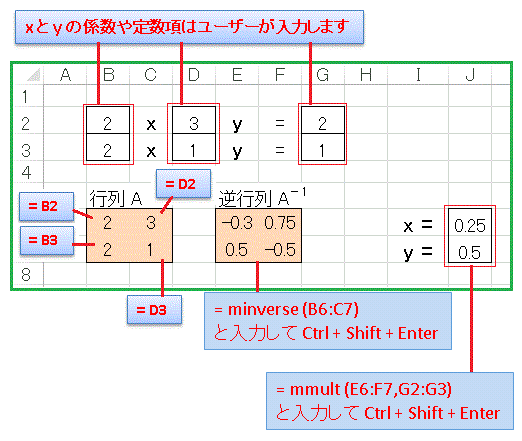
セル B2, B3, D2, D3, G2, G1 には適当な値を入れておきます。セル B6, B7, C6, C7 には相対参照で方程式の x と y の係数を写し取るようにして配列を作ります（ユーザーが値を変えれば配列も変化します）。
 
次に逆行列を作ります。セル B6 から C7 の範囲を選択して

=minverse(B6:C7)

と入力して、[Ctrl] + [Shift] + [Enter] を押してください。次に行列積を計算します。セル I6 と I7 を選択して

=mmult(E6:F7,G2:G3)

と入力して、[Ctrl] + [Shift] + [Enter] で解を得ます。ご自身で係数の値を色々変えて、解がどう変化するかを確認してください。