一般に虚数 i が数学世界で市民権を得るようになったのは 16 世紀に 3 次方程式の解法が確立されたときです。 3 次方程式ではたとえ結果が実根であったとしても、複素数の計算を経由しなくては解けなかったからです。この 3 次方程式の解法をめぐってタルタリアとカルダノという2人の人物がドラマを繰り広げます。
タルタリアとカルダノ
16 世紀のヨーロッパ、それは現代日本からは想像できないほど理不尽で残酷な暴力が溢れていた世界です。タルタリアもそのような世界で生まれ、そしてわずか 6 才のときに侵攻してきたフランス兵からひどい暴力を受けて一生口が聞けないほどの酷い怪我を負わされました。タルタリアとは本名ではなく「口がきけない」という意味のあだ名です(本名はニコロ・フォンタナ:Niccolo Fontana)。このあたりの人権感覚も現代とは全く異なるので、結局はこのあだ名が後世まで残ってしまいました。このような悲惨な境遇にも関わらず、彼は独学で数学を学び、1521 年には 22 歳でベロナで数学教師となります。 34 年にはベローナで教鞭をとるようになり、その 1 年後に 3 次方程式の解法を発見したと言われています。
ジェロニモ・カルダノ
ジェロニモ・カルダノ(Geronimo Cardano)はタルタリアよりも少しあとの 1501 年に生まれました。彼もまた自らが「母の堕胎の失敗により我が人生が始まった」と自嘲するほどの境遇にありましたが、苦学してパドバで医師となります。いっぽうで数学者としても並外れた才能をもっており、やはり 3 次方程式の解法の発見に並々ならぬ熱意をもっていたようです。彼が天才であることは認められていましたが、その悲惨な生い立ちが影響したのか極度の虚言癖があり、その人格は周囲から信用されていなかったようです。
カルダノはタルタリアに接近する
3 次方程式の解法を発見したタルタリアのもとにはその解法を伝授してほしいという人が次々と押し寄せていました。そのなかにはカルダノも混じっていたのです。彼はタルタリアに対して
「どうしても解法が知りたいのだ。頼む。教えてくれ。他には誰も喋らん。誓ってもいい」
と必死に懇願します。ついにタルタリアは根負けし、彼に解法を教えてしまいました。
カルダノの裏切り
その後、カルダノとその弟子ルドヴィコ・フェラーリは思わぬものを発見します。それはタルタリアの師であるシピオーネ・デル・フェッロという人物が書いた未発表論文でした。カルダノとは別に 3 次方程式を独力で導き出している内容で、しかもその日付はタルタリアによる発見よりも以前のものでした。
「となると … あの誓約は無効ということになるよな、ルドヴィコ君?」
「ええ、そりゃもちろんですよ、先生。へっへっへ」
という会話が師と弟子の間で交わされたかどうかわかりませんが、カルダノは『アルス・マグナ』という著書の中に 3 次方程式の解法を載せてしまいます。
タルタリアの反撃
カルダノの背信行為を知ったタルタリアは当然激怒し、カルダノに(互いに問題を出しあう)数学試合を申し込みます。当時は数学の世界にもこのような妙な習慣がありました。しかしカルダノはタルタリアの剣幕に怯んだのか、
「わしが出るまでもない。おい、ルドヴィコ君、軽くひねってやれ」
と弟子のフェラーリを代わりに対決させます。しかしこの弟子のフェラーリ、師をしのぐほどの天才的数学者で、4 次方程式の完全な解法を見つけた人物でもあります。また2人よりも年齢も若く油の乗った時期でもありました。タルタリアをこてんぱんに打ち負かし、結果として大きな名声を得ることになりました。結局、タルタリアとカルダノの争いで本当の勝利を収めたのはこのフェラーリだったのかもしれません。
タルタリアの三角形
次のような連続数について成り立つ足し算の規則をタルタリアの三角形とよびます。
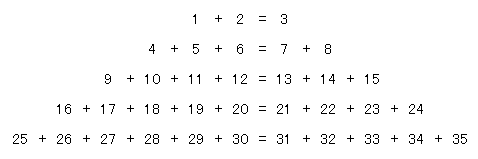
証明は簡単です。一般的な証明に入る前に、具体例として $n=3$ 段目の足し算
\[9+10+11+12=13+14+15\]
を見てみると、左辺については次のように書き直せます。
\[(9+9+9+9)+(1+2+3)=(3+1)\times 3^2+(1+2+3)\]
また、右辺は次のように書けます。
\[13+14+15=(4^2-3)+(4^2-2)+(4^2-1)=3\times 4^2-(1+2+3)\]
同様にして、第 $n$ 段目の左辺は $n^2$ から $n+1$ 個の連続数の和なので、
\[\begin{align*}(n+1)n^2+\sum_{k=1}^{n}k&=(n+1)n^2+\frac{n(n+1)}{2}\\[6pt]
&=\frac{n(n+1)(2n+1)}{2}\end{align*}\]
となります。また、第 $n$ 段目の右辺は $(n+1)^2$ から $n$ 個の連続数の和なので、
\[\begin{align*}n(n+1)^2-\sum_{k=1}^{n}k&=n(n+1)^2-\frac{n(n+1)}{2}\\[6pt]
&=\frac{n(n+1)(2n+1)}{2}\end{align*}\]
となって、左辺と右辺が一致することが確かめられました。

エクセルや数学に関するコメントをお寄せください
【AI連載小説】数学のリズム、エクセルの旋律(46)
「月子がタルタリアとカルダノについてレポートを書いています」
月子は一人で図書館の一角に座り、タルタリアとカルダノに関するレポートをまとめる作業に取り掛かっていた。彼女は口ごもりながら思考をまとめていく。
「タルタリアとカルダノ、二人ともルネサンス時代の数学者で、数学の発展に大きな貢献をしたんだ。まず、タルタリアは16世紀のイタリア出身の数学者で、特に代数学や方程式の解法において優れた手腕を持っていたわね」
月子はキーボードをたたきながら、検索した情報を元に続けた。
「彼はカルダノとの論争で知られているけど、その中でカルダノが解くことができなかった立方体方程式を解く方法を示し、それが後に解法の一翼を担うことになった」
彼女は考え込みながら次に進んでいった。
「カルダノもまた、同じ時代の数学者で、タルタリアと同じく代数学の分野で重要な業績を残しているわ。彼の名前は、カルダノの解法によって解かれることができる立方体方程式にちなんでいますね。これらの数学者たちは、当時の数学において競い合いながらも、新しい概念や方法を提案し、数学の進歩に寄与したんだ」