閉区間に含まれる要素数

関数とは数と数を１対１の対応で結びつけるものです。中学校では最初に一次関数 y = ax というものを学びます。一見すると単純極まりない関係に思えますが、そこには身震いするような真実が隠されているのです。

閉区間に含まれる要素数

一次関数 y = 2x のグラフを描いてみます。
 

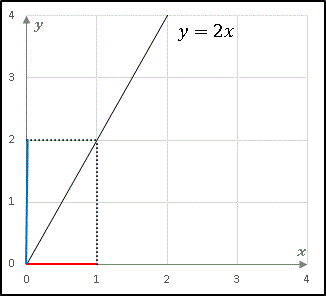
グラフには x 軸に沿った区間 [0, 1] を赤い線分で、y 軸に沿った区間 [0, 2] を青い線分で示してあります。さて、赤い部分と青い部分、どちらによりたくさんの数が含まれているでしょうか？　なんだか馬鹿げた問いに思えますね。
「青い線分は赤い線分の２倍の長さがあるのだから、含まれている数も２倍あるはずだ」
と考えるのが普通です。

しかし本当にそうでしょうか？
まず x から y への対応関係を考えます。これは関数なのですから、x が整数であろうと有理数であろうと、あるいは無理数であろうと、必ず対応関係がつきます。でも x を取りつくしたあとに右の図のように y が余ってしまうこともあるかもしれません。そこで y = 2x を x = y/2 と書き換えて、先に y を定めてから x を決めることにします。この場合も１つの y に対して１つの x が対応するので、x と y は必ず１対１で結びつき、どちらかが余るということはありません。したがって

 区間 [0, 1] と区間 [0, 2] に含まれる要素数は同じである

と結論できます。「そんな馬鹿な！」と思われるかもしれませんが、数学においては、これは全くの真実です。数直線のある部分を切り取ると、そこには必ず無限の要素が含まれます。つまり無限集合同士を比較しているので、このような直感に反した結論が導き出されてしまうのです。上の例では y = 2x という関数で調べましたが、x の係数を変えて y = 10 x にしようが y = 100 x にしようが同じことです。つまり区間 [0, 1] や区間 [0, 10] , あるいは区間 [0, 100] も、そこに含まれる要素数は同じであるということです。さらに一般的に言うと、

 数直線から適当な閉区間を切り取れば、そこに含まれる要素数はどれも同じである

ということです。この議論をさらに無限に広がる平面にまで拡張したのがリーマンという数学者です。