久しぶりの「数学よもやま話」です。今回はあの有名なアキレスとカメのパラドックスのお話です。ただし、当記事の結論部分はすべて私の個人的な仮説です。あくまで考え方の一つとしてとらえてください。
アキレスと亀のパラドックスについて考察します
「アキレスとカメのパラドックス」では、足の速いアキレスがカメと徒競走します。もちろん普通に競争したのでは勝負になるはずもありませんからハンデをつけます。アキレスはカメよりずーっと後ろのほうからスタートすることになります。ハンデの距離やゴール地点の位置によって勝敗は様々でしょうけど、そんなことは脇に置いておきます。ちょっと下図を見てください。
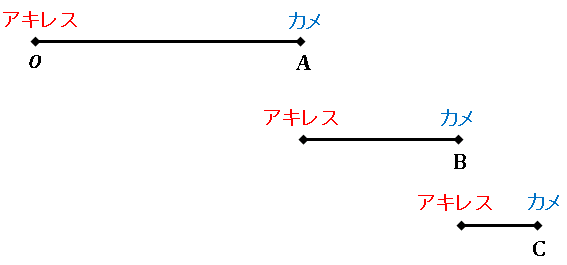
アキレスはカメとの距離をどんどん縮めていきます。
アキレスはやがてカメのスタート地点 A に辿り着くはずです。しかし、カメもその間に少しは前に進んでいるはずで、このときのカメの位置を B とします。アキレスはまた走って B に達しますが、その間にカメは C に達しています。そこでまたアキレスはまた走って C に ……. あれ? こんなことを永遠に繰り返していては、いつまでたってもアキレスはカメに追いつけませんよ。いったいどういうことなのでしょう? これが「アキレスとカメのパラドックス」です。
このパラドックスを初めて見る人は「ああでもない、こうでもない」としばらく考えてみてください。でも、このままではちょっと考えにくいので、問題の本質を変えないように少しだけアレンジしてみます。アキレスとカメの相対距離に着目してそれを棒グラフで表してみます。
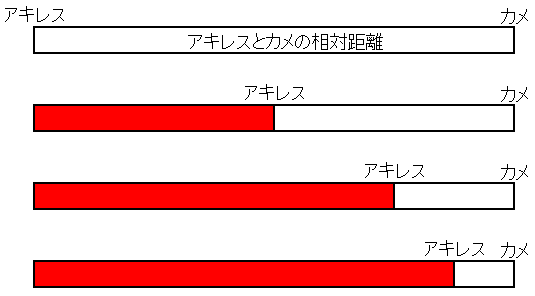
白い部分がカメとの間にある距離、赤い部分はすでに縮めた距離です。
アキレスはある時点で最初に離れていた距離の半分に達するはずですね。
さらに時間が経過すると、そのまた半分の距離を縮めます。
そしてまた時間が経過すると、そのまた半分の距離を縮めて …
半分、半分、また半分 … と無限に繰り返されます。
「アキレスとカメ」は古代ギリシアのゼノンという哲学者が考案したパラドックスです。現代では数学の抽象化が進み、自然科学はその近似的モデルの構築するために数学を用いるという考え方が基本ですが、古代ギリシアでは「数学 = 自然界の法則」と考える傾向が強かったので、このパラドックスは数学と物理学の両方に対する問題提議と捉えてよいと思います。
まずは数学的解決法から見ていきます。数学では公理(なにものからも証明されない自明の事実)として実数が連続であることを決めています。つまり実数直線は際限なく小さく分割することができます。このような前提のもとに微分積分という学問は組み立てられています。とにかく数学の問題であれば級数の計算で「アキレスとカメのパラドックス」を完全に解決できます。
アキレスが相対距離を 1/2, 1/4, 1/8 … と縮めていくので、
1/2 + 1/4 + 1/8 + 1/16 + 1/32 …
という無限に続く足し算を行うのですが、これは級数の初等的な問題で、
1/2 + 1/4 + 1/8 + 1/16 + 1/32 … = 1
と計算できることが知られています。
これは小さな数を次々と足していって、塵も積もれば 1 となるということを表した式なのですが、この「無限に足す操作」は、あくまで距離に関する足し算であって、逆の見方をすれば、アキレスとカメの相対距離 1 を無限に切り分けたというだけのことです。これは時間とは一切関係ありません。距離が無数に分割されるからといって、その距離を通過するのに無限の時間がかかるというわけではないのです。つまり「いつまでたっても追いつけない」という言葉自体、空間に対する無限分割操作と時間の無限を混同してしまっているので、ちょっと問題提議の仕方に無理があるように思えます。
さらにもう少し細かいことを言うと、数学においては時間という概念は存在しないので、仮に自然界の距離や時間を x(t) = vt という形で投影させるにしても、数学的にいえば 2 つの実数の集合 x, t 同士を結びつけた関数でしかないということです(横軸に t, 縦軸に x をとれば直線グラフになります)。適当な t をとればカメのいる位置を追い越したところにアキレスは存在することになります。
これが物理学(つまり現実世界)の話になると、事情は全く違ってきます。極微の世界を扱う量子力学では、物質の位置は波動関数とよばれる確率の波で表されます(正確には二乗すると位置の確率を表す関数)。つまり、測定するまで物質がどの位置にあるかわかりません。また、物質の位置を測定した瞬間に、速度や方向の情報が失われるという奇妙な性質をもっています。
仮にアキレスが電子のような小さな粒子だとしたら、ある時点で観測してその位置を把握すると、その瞬間にアキレスはどの方向を向いているのか、どれだけの速度で歩いているのか全くわからなくなってしまうということです。したがって、このパラドックスの「アキレスが一定方向に進む」という前提条件自体が無意味になります。また、現代物理学では空間に最小単位があるという説が有力なので、「空間を限りなく分割する」という前提も成り立たないかもしれません。
もちろん、人間のような巨視的物体(原子の集合体)はカメを追い越します(古典力学では等速運動を x=vt という単純な式で表します)。それがなぜなのか、また、微視的世界(ミクロ系)と巨視的世界(マクロ系)の境目がどのあたりにあるのかを突き詰めると、とても難しい問題のようです。私も最近「量子力学 古典力学 適用 境目」のようなキーワードで検索して色々調べていますが、頭が混乱するばかりです。この点について詳しい方にコメントしていただけるとありがたいです。よろしくお願いします。

エクセルや数学に関するコメントをお寄せください
昔、1/2 + 1/4 + 1/8 + 1/16 + 1/32 … = 1を、子供にも直感的に理解してもらうために、正方形の折り紙を使い、最初に正方形を対角線で切った三角形を置き、次に残りの三角形を半分に切って置き、次に残りの・・を続けていくと、どんどん元の正方形に近付いていく、という説明を考えたことがあります。
まぁ、その程度の説明は、きっと誰かがとっくに考えているんだろうなぁと思いますが。
面白いです! こんなふうに視覚に訴えると、直感的に無限の世界に触れることができて楽しいですね。
こんなふうに視覚に訴えると、直感的に無限の世界に触れることができて楽しいですね。
さっそく、Excel で描いてみました。
こんな感じですかね。
量子力学の適用される極微の世界においてはからの説明が間違ってます。具体的には、ゼノンのパラドックスはパラドックスではありませんでした。時間を無限に切り取って、矢を観測し続けると(実際には矢じゃなく、電子とか)その状態を維持し、状態の変化を阻止します(時間の凍結)。観測した瞬間、速度や方向という情報が欠落し、静止する(波動関数の収束)。アキレスの矢でとらえれば、無限に観測するため、止まってしまいます(ゼノン量子効果で調べればわかると思います)
ご指摘ありがとうございます。
いい加減な記事を書いて申し訳ありませんでした。
今、ゼノン量子効果について調べています。
近いうちに記事を修正したいと思います。
いい加減な記事を書いて申し訳ありませんでした。>いえ、数学における、極限(操作)と、微積のことを書きたかったんだろーなーって思っています。私の考えでは、数学における極限や微積は、直観と比較的一致するものであるが、こと量子において、直観と現象(実験結果)がそもそもいっちしない。数学的な発想では、そこから抜け出せないのではと思ったので、書いただけです。アキレスの矢は、数学的な考えでは矛盾するが、量子的には、量子ゼノンパラドックスだったのが、量子ゼノン効果と、格下げになっています。ちなみに、アインシュタインは、物質に確率を使うのを否定していたが、計算道具として便利だって言ってます。私も同じ意見です。修正、楽しみにしています(量子の部分だけだと思うので、まともにやるとドツボにはまると思うので、無理しない程度に( ´∀` ))
【AI連載小説】数学のリズム、エクセルの旋律(41)
「エクセルでアキレスと亀のパラドックスを表現してみよう」
真琴:「みんな、新しいプロジェクトのアイディアがあるんだ。アキレスと亀のパラドックスをExcelでどう表現するか考えてみないか?」
研伸:「アキレスと亀? ああ、あの逐次的な走りっぷりが有名なやつだね。でも、Excelってどうやって表現するんだ?」
真琴:「アキレスと亀が走る過程を、セルや数式を使って表現してみようって思ってさ」
月子:「面白いね。アキレスが亀に追いつく瞬間とか、どう表現するつもり?」
真琴:「それが難しいんだよね。理論的には追いつく瞬間が存在するはずなんだけど、具体的に表現するって難しいんだよ」
研伸:「Excelだと、セルの更新って離散的だもんな。連続的な瞬間をどう表現するか、ってことか」
真琴:「そうそう。アキレスと亀の位置を時間の経過に合わせてどう更新するか、ってのが課題だよ」
月子:「計算機的な表現においては、連続的な瞬間を表現するって難しいよね」
真琴:「でも、それが面白いところでもある。Excelを通じて、このパラドックスの数学的な側面や限界に迫っていけたらいいなと思ってるんだ」
研伸:「なるほど、面白い挑戦だね。それでは、アキレスと亀のExcel表現、どんな数式やセルの使い方が考えられるか、アイディアを出し合ってみようじゃないか」
真琴:「さて、アキレスと亀のパラドックス、どうやって表現しようかな」
研伸:「まずは、アキレスと亀の初期位置を設定しよう。どこからスタートするか考えないとね」
真琴はエクセルのA列に「アキレスの位置」、B列に「亀の位置」という見出しをつけ、初期位置をセルに入力しました。
月子:「じゃあ、どんな速さで動くかも考えないといけないね」
真琴:「そうだね。速さも重要だ。エクセルのC列に「アキレスの速さ」、D列に「亀の速さ」を追加しよう」
三人は速さの初期値を入力し、数式を用いて時間の経過に伴う位置の変化を計算するセルを用意しました。
研伸:「でも、エクセルは離散的だから、瞬間的な追いつきって表現できるのかな」
月子:「確かに難しい問題だね。どうやって連続的な瞬間を表現するかがポイントだよ」
真琴:「そこが難しいんだよね。でも、時間を小さな単位で刻むことで近似的に表現することはできそうだ」
三人は時間を小刻みに進め、アキレスと亀の位置が一致する瞬間や、アキレスが亀を追い越す瞬間を見つけるためにセルの数式や条件付き書式を工夫していました。
研伸:「これで、エクセル上でアキレスと亀の動きを追いかけることができそうだね」
月子:「確かに面白そう。アキレスが亀を追い越す瞬間や、一致する瞬間を見つけるのはどうやるか、進めながら試していくといいかもしれないね」