平面上の動点が目的地に辿り着くまでの最短時間

【CL26】動点が目的地に到達するまでの最短時間

$xy$ 平面上に動点 $P$ があります。$P$ は $x$ 軸上では速さ $a\;(\gt 1)$ で、それ以外のところでは速さ $1$ で移動します。このとき動点 $P$ が $y$ 軸上の点 $A\,(0,\:1)$ から $x$ 軸上の点 $B\,(2,\:0)$ へ行くまでに要する 最短時間 を求めてください。（千葉大一部改）
　




【ヒント】もし動点の速さが平面上のどこでも一定であれば、$A$ から $B$ へ直線で移動するのが最短に決まっています。しかし、問題の設定では $x$ 軸上では速度を増すので、$a$ の値によっては途中で $x$ 軸に下りたほうが点 $B$ に早くたどり着くかもしれません。その $x$ 軸上の点を見つけるのが本問のポイントとなります。
　
【解答】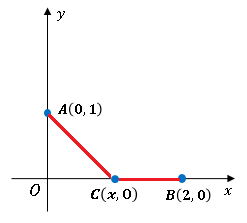　図のように点 $C(x,\:0)$ を経由して点 $B\,(2,\:0)$ へ向かうとします ($x=2$ なら直線経路)。
\[AC=\sqrt{1+x^2},\quad CB=2-x\]
なので、点 $C$ までの所要時間は速さが $1$ なので
\[\sqrt{1+x^2}\]
となります。$x$ 軸上では速さが $a\;(\gt 1)$ なので、点 $C$ から $B$ までの所要時間は
\[\frac{2-x}{a}\]
となります。よって $A$ から $C$ までの所要時間は合わせて
\[f(x)=\sqrt{1+x^2}+\frac{2-x}{a}\]
となります。$f(x)$ を微分すると
\[f'(x)=\frac{x}{\sqrt{1+x^2}}-\frac{1}{a}\]
$f'(x)=0$ となる $x$ を求めると
\[x=\frac{1}{\sqrt{a^2-1}}\]
となります ($a\gt 1$ なので分母は常に正となります)。$f(x)$ の二階微分を計算すると
\[f^{\prime\prime}(x)=\frac{1}{(1+x^2)^{3/2}}\gt 0\]
なので $f(x)$ のグラフは下に 凸 です。

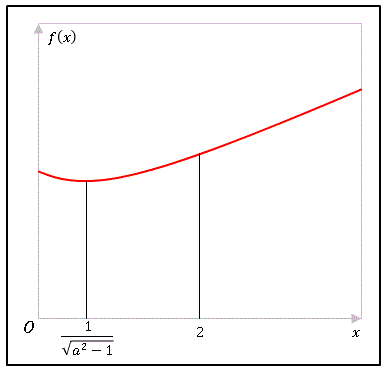
$f(x)$ の極値は $a$ の値によって変化するので、極値が $0$ から $2$ の範囲内にあれば、その最小値は上の図にあるように $f(x)$ の極値と一致しますが、極値が $2$ より大きければ最小値は $f(2)$ となります（つまり直線経路です）。したがって
\[\frac{1}{\sqrt{a^2-1}}\leq 2,\quad a\gt 1\]
すなわち $\displaystyle 1\lt a\leq\frac{\sqrt{5}}{2}$ のとき、最小値は
\[f\left(\frac{1}{\sqrt{a^2-1}}\right)=\frac{\sqrt{a^2-1}+2}{a}\]
となります。また
\[\frac{1}{\sqrt{a^2-1}}\gt 2\]
すなわち $\displaystyle a\gt\frac{\sqrt{5}}{2}$ のとき、最小値は
\[f(2)=\sqrt{5}\]
となります。以上まとめると最短の所要時間 $T$ は
\[T=\begin{cases}\displaystyle\frac{\sqrt{a^2-1}+2}{a} & \left(1\lt a\leq\displaystyle\frac{\sqrt{5}}{2}\right)\\[6pt]\sqrt{5} & \left(a\gt\displaystyle\frac{\sqrt{5}}{2}\right)\end{cases}\]
となります。