【確率】部屋割り・図形の塗り分け・格子点の結び方

【PS06】部屋割りの仕方を数えます

$n$ 人を部屋割りします。
１つの部屋には少なくとも１人は入れるものとして以下の問いに答えてください。
(1) $n\geq 2$ とします。$n$ 人を $2$ 室に入れる方法は何通りありますか。
(2) $n\geq 3$ とします。$n$ 人を $3$ 室に入れる方法は何通りありますか。
(3) $n\geq 4$ とします。$n$ 人を $4$ 室に入れる方法は何通りありますか。

【ヒント】シンプルな設定ですが、このタイプの問題を初めて見る場合は意外に手こずるかもしれません。考え方さえわかれば計算自体は簡単です。(2) は (1) の結果を、(3) は (1) と (2) の結果を使います。

【解答】部屋に人がいる場合を A , 空室を X という記号で表すことにします。

(1) $n$ 人が無条件で部屋を選択できる場合は重複順列なので $2^n$ 通りですが、空室を作ってはいけないというルールなので、

XA　AX

という $2$ 通りを除かなくてはいけません。よって答えは $2^n-2$ 通りです。

(2) 無条件で部屋を選択できる場合は $3^n$ 通りです。$1$ 室が空室になるような状況、すなわち

XAA　AXA　AAX

という状況は、それぞれについて $2$ 部屋に空室のないように入れる仕方の数をかぞえればよいので、(1) の結果より全部で $3\,(2^n-2)$ 通りです。また、$3$ 室のうち $2$ 室が空室となるのは

XXA　XAX　XXA

の $3$ 通りです。以上より答えは
\[3^n-3\,(2^n-2)-3=3^n-3\cdot 2^n+6\]
となります。

(3) 無条件で部屋を選択できる場合は $4^n$ 通りです。$1$ 室が空室になるような状況、すなわち

XAAA　AXAA　AAXA　AAAX

という状況は、それぞれについて $3$ 部屋に空室のないように入れる仕方の数をかぞえればよいので、(2) の結果より全部で
\[4\,(3^n-3\cdot 2^n+6)\;通り\]
あります。$1$ 室が空室になるような状況は $4$ つの異なるものから $2$ つを選ぶので ${}_{4}\mathrm{C}_{2}=6$ 通りです：

AAXX　AXXA　XXAA　XAAX　XAAX　XAXA　AXAX

それぞれについて $2$ 部屋に空室のないように入れる仕方の数をかぞえればよいので、(1) の結果より全部で
\[6\,(2^n-2)\;通り\]
あります。また、$4$ 室のうち $3$ 室が空室となるのは

XXXA　XXAX　XAXX AXXX

の $4$ 通りです。以上より答えは
\[4^n-4\,(3^n-3\cdot 2^n+6)-6\,(2^n-2)-4=4^n-4\,\cdot 3^n+6\,\cdot 2^n-16\]
となります。

【PS07】n 種類の色で四角形を塗り分けます

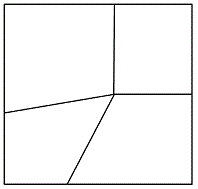　異なる $n$ 種類の色 ($n\geq 4$) からいくつかの色を選んで右の図形の各四角形を塗り分けます。ただし、互いに辺を共有する $2$ つの四角形には異なる色を塗るものとします。塗り分け方は何通りありますか。（大阪府大一部改）



【ヒント】何色で塗り分けるかによって場合分けします。辺を共有する四角形に同じ色を塗れないことに注意してください。

【解答】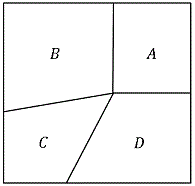図のように各四角形を $A,\;B,\;C,\;D$ とします。

[1] $4$ 色で塗る場合は $n$ 種類から $1$ 色を選んで $A$ に塗り、残り $n-1$ 色から $1$ 色選んで $B$ に塗り … とすればよいので、
\[n(n-1)(n-2)(n-3)\;\verb|通り|\]
となります。

[2] $3$ 色で塗る場合、まず $n$ 種類から $3$ 色を選ぶ方法は
\[{}_{n}\mathrm{C}_{3}=\frac{n(n-1)(n-2)}{6}\;\verb|通り|\]
です。この $3$ 色から $2$ 色を選んで $A,\;C$ に塗り、残りの $1$ 色を $B,\;D$ に塗る方法は $3\times 2=6$ 通り。同様に、$3$ 色から $2$ 色を選んで $B,\;D$ に塗り、残りの $1$ 色を $A,\;C$ に塗る方法も $6$ 通りです。したがって、 $3$ 色で塗る場合の数は
\[2\times 6\times\frac{n(n-1)(n-2)}{6}=2n(n-1)(n-2)\;\verb|通り|\]
となります。

[3] $2$ 色で塗る場合、$n$ 種類から $2$ 色を選ぶ方法は
\[{}_{n}\mathrm{C}_{2}=\frac{n(n-1)}{2}\;\verb|通り|\]
$2$ 色のうち $1$ 色を $A,\;C$ , もう $1$ 色を $B,\;D$ に塗る方法は $2$ 通りです。
よって $2$ 色で塗る場合の数は

\[2\times\frac{n(n-1)}{2}=n(n-1)\;\verb|通り|\]
となります。以上 [1][2][3] をまとめると色の塗り方は

\[\begin{cases}n(n-1)(n-2)(n-3)\;\verb|通り| & (\verb|4色で塗る場合|)\\[6pt]
2n(n-1)(n-2)\;\verb|通り|& (\verb|3色で塗る場合|)\\[6pt]
n(n-1)\;\verb|通り| & (\verb|2色で塗る場合|)\end{cases}\]
となります。

【PS08】格子点を結んで三角形を作ります

　右の図のように、碁盤の目に並んでいる $16$ 個の点から $3$ 個の点を選んで、それらを頂点とする三角形を作ります。全部でいくつの三角形ができますか。






【ヒント】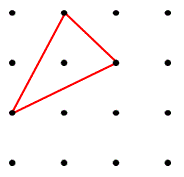　右図のように適当に $3$ つの点を選んで三角形を作ります。しかし、中には三角形を作れない点の選び方もあることに注意します。

【解答】$16$ 個の格子点から $3$ 個を選ぶ方法は
\[{}_{16}\mathrm{C}_{3}=560\;通り\]
ですが、$3$ 点が一直線に並んでいると三角形が作れないので、そういう選び方は除く必要があります。下の図にあるように、$4$ 点が直線上に乗るような線の引き方は、縦に $4$ 本、横に $4$ 本、斜めに $2$ 本の合計 $10$ 本です。

それぞれの直線上にある $4$ 点から $3$ 点を選ぶ方法は ${}_{4}\mathrm{C}_{3}$ 通りなので、これらの直線上から $3$ 点を選ぶ方法は全部で

\[{}_{4}\mathrm{C}_{3}\times 10=40\;通り\]
となります。次に $3$ 点が一直線に並ぶような状況は下の図にあるように、合計 $4$ 本です。



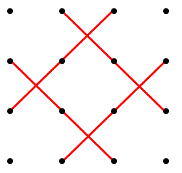
以上より、格子点を結ぶ三角形は全部で
\[560-40-4=516\;個\]
あります。