角度比の極限値

【CL07】角度比の極限値

図のように１直線上に３点 $O\:,A,\:B$ をとり、$OA = 1,\:AB = 2$ となるようにします。また $O$ を通って $OA$ に垂直な直線上の動点を $P$ とします。
 

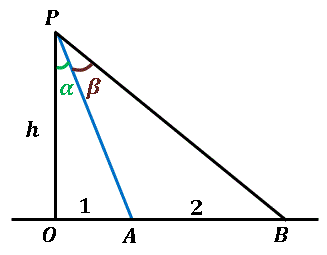
　$OP=h,\:\angle OPA=\alpha,\:\angle APB=\beta$ とするとき、$\displaystyle \lim_{h \rightarrow \infty}\frac{\alpha}{\beta}$ を求めてください。（千葉大）

【ヒント】角度比の極限値を求める問題です。底辺 OB を円弧とみれば答えを予測できます。
　
【解答】$h$ を無限に大きくすると、$OA$ と $AB$ は 無限大半径をもつ円の円弧 とみなすことができます。つまり $OA$ と $AB$ は円周角 $\alpha$ と $\beta$ の比である 1：2 となっていることが予測されます。それでは実際に解答を作って確認してみましょう。すぐに三角関数の極限公式を使うことを思いつくはずです。$\sin x$ に関する公式を用いても解答できますが、斜辺を平方根で表すのが大変なので、ここは $\tan x$ の極限公式
 \[\lim_{x\rightarrow 0}\frac{\tan x}{x}=1\tag{1}\]
を使うことにします。問題図から
 \[\tan \alpha=\frac{1}{h},\quad\tan(\alpha+\beta)=\frac{3}{h}\tag{2}\]
という関係式が得られるので、 $h \rightarrow \infty$ のとき、
 \[\lim_{h\rightarrow\infty}\tan\alpha=0,\quad\lim_{h\rightarrow\infty}\tan \beta=0\]
となります。すなわち $h\rightarrow\infty$ のとき
 \[\alpha\rightarrow0,\quad\beta=\rightarrow0\]
となって公式 (1) が使えることがわかります。すなわち
 \[\lim_{h \rightarrow\infty}\frac{\tan\alpha}{\alpha}=\lim_{\alpha \rightarrow 0}\frac{\tan\alpha}{\alpha}=1\]
です。ここで $\alpha$ と $\beta$ の比をとって
 \[\frac{\alpha}{\beta}=\frac{\alpha}{\tan \alpha}\,\frac{\tan \alpha}{\tan \beta}\,\frac{\tan \beta}{\beta}\]
と半ば強引に変形して極限公式が使えるようにします。つまり $\tan \alpha$ と $\tan \beta$ の比が求まれば答えが得られることがわかります。しかし、まだ $\tan \beta$ の値が分からないので加法定理から
 \[\tan\beta=\tan\{(\alpha+\beta)-\alpha\}=\frac{\tan(\alpha+\beta)-\tan \alpha}{1+\tan(\alpha+\beta)\tan\alpha}\]
という式をつくってから (2) を代入すると
 \[\tan\beta=\frac{2h}{h^2+3}\]
が得られます。よって求める極限は
 \[\lim_{h\rightarrow \infty}\frac{\alpha}{\beta}=\lim_{h \rightarrow\infty} \left(\frac{\alpha}{\tan\alpha}\,\frac{\tan\alpha}{\tan\beta}\,\frac{\tan\beta}{\beta}\right)=1\cdot\ \frac{1}{2}\cdot\ 1=\frac{1}{2}\]
となります。