複素平面上の直線方程式

【CX05】複素数平面上の直線方程式

(1)複素数平面上の $2$ 点、$\alpha=a+ib$ と $\beta=c+id$ を通る直線の方程式を $z=x+if(x)$ の形で求めてください。
 
(2) 複素数平面上の原点と $1+i$ を結ぶ直線の方程式を求めてください。
 
【ヒント】$x$ と $y$ の関係を求める問題です。

【解答】(1) まず状況を複素数平面に描いてみます。
 

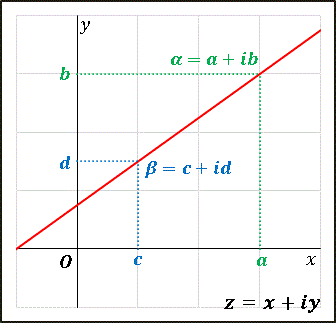
複素数平面上であっても、$x$ と $y$ の関係に着目すると、普通の $xy$ 平面における直線方程式と同じです。なので、
 \[(a-c)(y-b)=(b-d)(x-a)\]
となります。これを $y=f(x)$ の形に書き直すと
 \[y=\frac{b-d}{a-c}\:x+\frac{ad-bc}{a-c}\]
となるので、$z-x$ の方程式として
 \[z=x+i\left[\frac{b-d}{a-c}\:x+\frac{ad-bc}{a-c} \right]\]
が得られます。

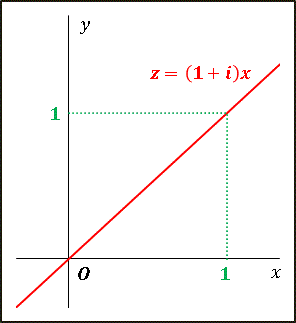
(2) $\alpha=1+i,\:\beta=0+0i$ とすると
 \[a=1,\:b=1,\:c=0,\:d=0\]
ですから、(1) の結果に代入して
 \[z=x+ix=(1+i)x\]
という方程式となります。
 
　

【CX06】実数でないことの証明

$p$ を素数、$(a,\:b)$ を互いに素な正数とするとき、$(a+b\:i)^{\,p}$ は実数でないことを示してください。$i$ は虚数単位です。（京大）

【ヒント】今回は京都大学理系の入試問題です。さすがにすらすら証明できるような問題ではありませんけど、２項展開が面倒であることを差し引けば、素直な手順で意外となんとかなります。３０分～１時間ぐらいかけて丁寧に解答してみてください。出だしには注意です。素数のなかでも 2 だけは偶数なので、いつも気を付けておきたいところですね。

【解答】$p=2$ のときは
 \[(a+bi)^2=a^2-b^2+2abi\]
となって虚部は $0$ とはなりません。$p\geq 3$ のときは $p$ は全て奇数となります。何はともあれ、まずは二項展開です。
 \[\begin{align*}f\equiv &(a+bi)^p\\[6pt]=&a^p+\binom{p}{1}a^{p-1}(bi)+\binom{p}{2}a^{p-2}(bi)^2+\binom{p}{3}a^{p-3}(bi)^3+\:\cdots\:\\[6pt]&+\binom{p}{p-2}a^{p-(p-2)}(bi)^{p-2}+\binom{p}{p-1}a^{p-(p-1)}+(bi)^p\end{align*}\]
必要なのは虚部なので、実部は $\mathrm{Re}f$ とだけ書いて分離します。以降、$i^2-1$ を $-1$ に置き換えてしまうと、かえってややこしくなるので、そのままにしておきます。
 \[\begin{align*}f=&(a+bi)^p\\[6pt]=&\mathrm{Re}f+\binom{p}{1}a^{p-1}(bi)+\binom{p}{3}a^{p-3}(bi)^3+\:\cdots\:+\binom{p}{p-2}a^2(bi)^{p-2}+(bi)^p\end{align*}\]
虚部を $bi$ で括ります。
 \[\begin{align*}f=&(a+bi)^p\\[6pt]=&\mathrm{Re}f+bi\left\{\binom{p}{1}a^{p-1}+\binom{p}{3}a^{p-3}+\:\cdots\:+\binom{p}{p-2}a^2(bi)^{p-3}+(bi)^{p-1}\right \}\end{align*}\]
したがって、$f$ の虚部は
 \[\mathrm{Im}f= b\left\{\binom{p}{1}a^{p-1}+\:\cdots\cdots\:+\binom{p}{p-2}a^2(bi)^{p-3}+(bi)^{p-1}\right \}\]
と書くことができます。$\mathrm{Im}f=0$ とおくと、$b\gt 0$ より
 \[pa^{p-1}=-\binom{p}{3}a^{p-3}(bi)^2-\:\cdots\:-\binom{p}{p-2}a^2(bi)^{p-3}-(bi)^{p-1}\]
ここで、$-(bi)^2=b^2$ で右辺を括ります。
 \[pa^{p-1}= b^2\left\{\binom{p}{3}a^{p-3}+\:\cdots\:+\binom{p}{p-2}a^2(bi)^{p-5}-(bi)^{p-3}\right\}\]
右辺は $b^2$ の倍数なので左辺も $b^2$ の倍数である必要があります。しかし $a$ と $b$ は互いに素なので、$p$ が $b^2$ の倍数でなければなりません。しかし、$p$ は素数なので $b=1$ だけが適合します。そこで改めて $b=1$ として $\mathrm{Im}f=0$ の方程式を書きなおすと
 \[pa^{p-1}+\binom{p}{3}a^{p-3}(i)^2+\:\cdots \:+\binom{p}{p-2}a^2(i)^{p-3}=-(i)^{p-1}\]
左辺は $z^2$ の倍数、右辺は $\pm 1$ なので $a=1$ とならなければなりません。したがって、 $\mathrm{Im}f$ が $0$ となる可能性があるのは $a=b=1$ だけですが、その場合も
 \[(1+i)^p=2^{p/2}\left(\cos\frac{\pi}{4}+i\:\sin\frac{\pi}{4}\right)\]
となって虚部は $0$ になりません。以上の議論より、$(a+bi)^p$ は実数にはなりません（証明終）。