今回はかなり難しい問題です。ひらめきというよりは、論理をコツコツと積み重ねて解くタイプの問題です。算数カテゴリの問題なので方程式を使わないで解いてみてください。
【算数問題64】三桁の数字の位を並び替えます
1 ~ 9 の数字から 3 つを取り出して ABC と並べて三桁の数字を作ります。ただし同じ数字のものはありません。A, B, C の数字を全て足し合わせると 14 でした。また、A, B, C の数字を並び替えてみると、最初の数字より 207 小さくなっていました。このような条件をみたす A, B, C の数字を求めてください。
【ヒント】少しずつ根気よく絞り込んでいきます。最初は 207 の “0” に着目して …
【解答64】まず ABC を並び替えた数を差し引いて十の位が 0 にることに着目し、仮に B が元の位置のままで A と C の位置だけが入れ替わった CBA という状態がありえるのかを考えてみます。筆算で表すと次のようになります。
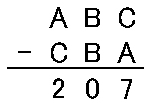
これは明らかにありえないですね。というのも、この計算が成立するには、一の位の引き算をするときに、となりの数字 B から 1 をとってくることはできないので、C > A でなければなりません。しかし百の位を見ると明らかに A > C をみたす必要もあります。これは矛盾するので、B の位置は動いているということがわかります。そこで改めて並び替えた数字を XYZ で表して、次のように書いてみます。
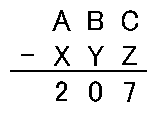
今この段階でわかっているのは B ≠ Y ということです。次は一の位に着目します。C から Z を差し引いて 7 になる可能性があるのは、
(C, Z) = (1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9)
ここで C > Z のような可能性はないことに注意します。たとえば (C, Z) = (9, 2) のようになっているのなら、B から Y を引くと 0 になってしまって、B ≠ Y という条件に反します。B から 1 を差し引いた値が Y となっていなくてはならないのです。
ここで「A, B, C の数字を全て足し合わせると 14」という条件を使うと、(C, Z) の候補から (6, 9) が消えます。そして C だけが確定した状態で、とりあえず 3 つの数字の組合せの候補がわかります。
(C, Z, ?) = (1, 4, 9), (2, 5, 7), (3, 6, 5), (4, 7, 3), (5, 8, 1)
元の数字と並び替えた数字は
491, 941 ⇒ XY4
572, 752 ⇒ XY5
653, 563 ⇒ XY6
734, 374 ⇒ XY7
815, 851 ⇒ XY8
のようになっています。そこでたとえば
491, 941 ⇒ XY4
を例にとって筆算で表してみると次のようになります。
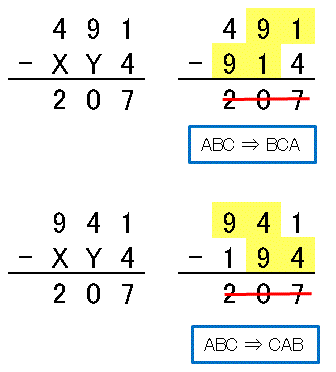
B ≠ Y という条件を使うと、図のように X と Y の値は自動的に決まります。上のケースでは計算式が成り立っていないので(つまり求める数字ではないので)、引き算の答えは赤い線で打ち消してあります。ここで確認したいのは並び替えのパターンです。図をみると並び替えには
ABC ⇒ BCA, ABC ⇒ CAB
という 2 つの可能性があることがわかります。黄色で網掛けしてある部分がスライドしています。ということは、求める数字は
B – C = 1, B – A = 1
のどちらかが成立しているはずです。残りの候補
572, 752, 653, 563, 734, 374, 815, 851
の中からそのような数字を探してみると 563 しかありません。実際に計算して確認してみると
563 – 356 = 207
となって、確かに問題の条件をみたしています。

エクセルや数学に関するコメントをお寄せください