ド・モルガンの法則

条件 $p,q$ について 「$p$ かつ $q$」を論理積（logical conjunction）とよび、「$p\wedge q$」と表します。「かつ」は英語の and です。「ともに」と言い換えるとわかりやすいかもしれません。たとえば実数 $x,y$ について $x^2+y^2=0$ が成り立つとき、$x$ と $y$ はともに $0$ なので、
$$x^2+y^2=0⟹x=0\wedge y=0$$
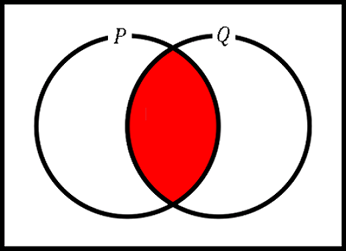
という命題は真です。$p,q$ を満たすものの集合をそれぞれ $P,Q$ とすると、$p\wedge q$ は $P\cap Q$ の要素となります。



条件 $p,q$ について 「$p$ または $q$」を 論理和 (logical disjunction) とよび、「$p\vee q$」と表します。英語の or に相当しますが、「どちらか一方」ではなく 「少なくとも一方は」 という意味であることに注意してください。たとえば実数 $x,y$ が $xy=0$ をみたすとき、$x$ と $y$ の少なくとも一方は $0$ となります：
$$xy=0⟹x=0\vee y=0$$
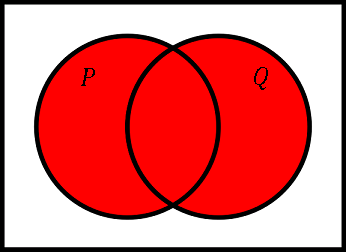
これは $x$ と $y$ のどちらか一方だけが $0$ でもよいし、両方が $0$ であってもよいという意味です。$p,q$ を満たすものの集合をそれぞれ $P,Q$ とすると、$p\vee q$ は $P\cup Q$ の要素です。

ド・モルガンの法則

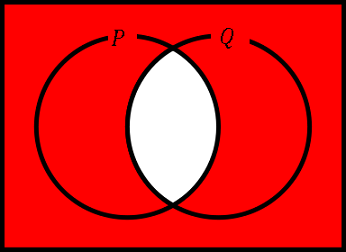
論理積の否定は $P\cap Q$ の補集合の要素となります。



したがって、「$p\wedge q$」の否定（否定論理積）は「$\overline{p}\vee \overline{q}$」（$p$ または $q$）となります。
$$\begin{array}{}\text{(1)}& \overline{p\wedge q}⟺\overline{p}\vee \overline{q}\end{array}$$
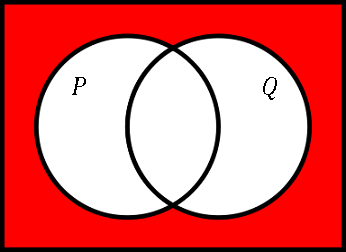
論理和の否定は $P\cup Q$ の補集合の要素となります。



よって、「$p\vee q$」の否定（否定論理和）は「$\overline{p}\wedge \overline{q}$」となります。
$$\begin{array}{}\text{(2)}& \overline{p\vee q}⟺\overline{p}\wedge \overline{q}\end{array}$$

(1) と (2) をまとめて ド・モルガンの法則（De Morgan’s Laws）とよびます：

論理積と論理和の例題を解いてみましょう。
【例題1】実数 $a,b$ について、次の命題
$$ab>0\wedge a+b>0⟹a>0\wedge b>0$$
の真偽を判定してください。
【解答】$ab>0$ ならば $a$ と $b$ が同符号です。すなわち「$a>0,b>0$」または「$a<0,b<0$」です。一方で $a+b>0$ をみたすには $a,b$ のうち少なくとも一方が正でなくてはなりません。したがって「$a>0,b>0$」となり、命題は 真 であることがわかります。

次の問題は 2015 年度センター試験の数学ⅠAで出題された問題を少し手直ししたものです。

【例題2】自然数 $n$ に対する条件 $p_1,p_2,q_1,q_2$ を次のように定めます。

 $p_1$：$n$ は素数
 $p_2$：$n+2$ は素数
 $q_1$：$n+1$ は $5$ の倍数
 $q_2$：$n+1$ は $6$ の倍数

$30$ 以下の自然数 $n$ のなかで命題$$p_1\wedge p_2⟹\overline{q_1}\wedge q_2$$の反例となる $n$ をすべて求めてください。

【解答】$p_1\wedge p_2$ は $n$ と $n+2$ がともに素数であることを意味します。これは互いに隣り合う素数、すなわち 双子素数 とよばれる組です。$30$ 以下の $n$ で双子素数 $(n,n+2)$ の組を並べてみると
$$(3,5),(5,7),(11,13),(17,19),(29,31)$$
の $5$ 組となります。一方、$\overline{q_1}\wedge q_2$ は $n+1$ は $5$ の倍数ではなく、$6$ の倍数となります。双子素数となる $5$ 組の $n+1$ は
$$n+1=4,6,12,18,30$$
ですから、このうち $6,12,18$ の $3$ 組は条件を満たしていますが、残りの $n+1=4,6$ は条件を満たしません。したがって $n=3,29$ が答えとなります。