統計学において、データ解析や関係性の評価に欠かせない指標として相関係数があります。相関係数は、2つの変数間の関連性を数値化することで、その関係性の強さや方向性を評価します。本記事では、相関係数の定義式や Excel での計算方法、解釈のポイントなどについて解説します。相関係数の理解を深めることで、データ分析の精度向上や予測能力の向上に役立てることができます。
標本相関係数
標本相関係数(ピアソンの積率相関係数)は2つのデータ同士の関連性の強さ(線型相関の程度)を表す数値です。大きさ $n$ の標本 $(x_i,\:y_i)$ については
\[C_{xy}=\frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2\sum_{i=1}^{n}(y_i-\bar{y})^2}}\]
という数式で表され、-1 から 1 の値をとるように定義されています。値が正のときは「正の相関がある」、負のときは「負の相関がある」と表現します。一般的に得られた数値の絶対値が大きいほどに種類のデータの関連性が強く、逆に 0 に近いほど関連性は薄いと考えます。大まかな目安として、次のような評価を行ないます。
・相関係数の絶対値 0.0 ~ 0.2 相関がほとんどない
・相関係数の絶対値 0.2 ~ 0.4 相関が少しある
・相関係数の絶対値 0.4 ~ 0.7 相関がかなりある
・相関係数の絶対値 0.7 ~ 1.0 強い相関がある
ただし、これはあくまで目安の指標なので、実際には全く関係のないデータ同士であっても「相関が少しある」のような結果が現れてしまうこともあります。
【Excel】CORREL関数・PEARSON関数
Excel には2つの配列の間の標本相関係数を計算する CORREL という関数が用意されています(全く同じはたらきをする PEARSON という関数もあります)。
=CORREL(配列1,配列2)
以下でサンプルデータを使って相関係数を計算してみます。
年齢と身長の相関係数
次の表は「6 歳から 18 歳までの男子を無作為に選んで身長を記録した」という想定で作成されたサンプルデータです。年齢と身長の間に相関があることは、ほぼ疑いのない事実ですが、その相関の強さがどれくらいなのか確かめてみましょう。
| 年齢 | 身長 [cm] |
|---|---|
| 6 | 117.66 |
| 7 | 123.90 |
| 8 | 128.88 |
| 9 | 133.90 |
| 10 | 139.73 |
| 11 | 145.89 |
| 12 | 153.32 |
| 13 | 160.93 |
| 14 | 166.33 |
| 15 | 169.45 |
| 16 | 170.50 |
| 17 | 171.74 |
| 18 | 171.77 |
上の表をコピーしてセル B2 に貼りつけてください。
表の体裁を整えてから、セル E2 に
=CORREL(B3:B15,C3:C15)
と入力します。
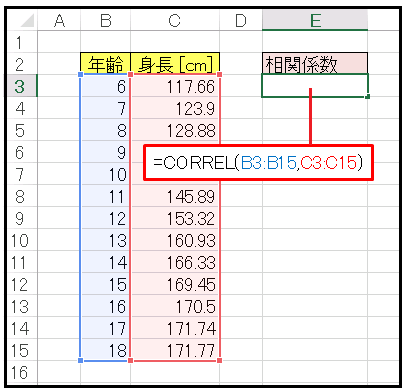
得られる値は 0.979 ですから、非常に強い相関があることがわかります。ただし年齢上限値を大きくすると、成人以降は身長が伸びないので相関は弱くなります。ちなみに年齢上限を 70 歳にしたときの相関係数は約 0.3 です。さきほどの指標で結論するなら「相関が少しある」という程度になってしまいます。CORREL 関数の代わりに PEARSON 関数を使って
=PEARSON(B3:B15,C3:C15)
と入力しても同じ結果が得られます。
乱数列同士の相関係数
次は乱数群同士の相関を調べてみます。乱数 A は 1 ~ 100, 乱数 B は 1 ~ 200 の範囲で出力された無作為な整数です。
| 乱数 A | 乱数 B |
|---|---|
| 27 | 188 |
| 92 | 149 |
| 88 | 20 |
| 2 | 90 |
| 23 | 25 |
| 81 | 15 |
| 31 | 105 |
| 8 | 158 |
| 55 | 114 |
| 80 | 57 |
こんなものに相関なんてあるわけない … そう考えるのが普通ですね。だって、デタラメな数なのですから。しかし、怖ろしい(?)結果が待ち受けています。上の表をコピーしてセル B2 に貼りつけてください。それから、どこでもいいので適当なセルに
=CORREL(B3:B12,C3:C12)
あるいは
=PEARSON(B3:B12,C3:C12)
と入力してください。「-0.363740446 」という負の相関が現れてしまいます。これは先ほどの指標では「相関が少しある」ということになります。70 歳を上限とした年齢と身長データの相関よりも大きな値です。これは相関係数があくまで「直線傾向の強さ」を表していることに起因します。たとえ乱数であっても下限値と上限値が近いと、これぐらいの相関を示します。ちなみに乱数 B の上限値を 1000 まで広げると、相関係数は約 0.1 まで下がります。

エクセルや数学に関するコメントをお寄せください