超関数とテスト関数・ディラックのデルタ関数

このページでは冒頭で超関数について簡単に触れ、その中のひとつであるディラックのデルタ関数について解説します。　

超関数とテスト関数

超関数の性質を調べるときには、テスト関数 $\varphi (x)$ というものを多用します。少し難しい表現になってしまいますが、テスト関数とは「台がコンパクトであり、何回でも微分可能な連続関数」のことです。「台」とは関数値が 0 でない定義域のことです。「コンパクト」は厳密に考えると難しいのですが、とりあえず「有界閉区間の集合である」と理解しておけば十分です。つまり「台がコンパクトである」というのは、$\varphi (\pm \mathrm{\infty })=0$ であることを意味しています。大雑把に次のような関数をイメージしてください。
 

このようなテスト関数 $\varphi (x)$ に対して
 $$\begin{array}{}\text{(A)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)f(x)dx\end{array}$$
が有限の値をとるような関数 $f(x)$ を超関数と定義します。超関数は普通の関数を拡張定義したものなので、二次関数や指数関数のような、ごく普通の関数も（上の積分は有限値をとるので）やはり超関数に含まれます。ただし、後述するデルタ関数のように、普通の関数とは明らかに異なる性質をもつ関数もその範疇に含まれることになります。そして
 $$\begin{array}{}\text{(B)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)f(x)dx={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)g(x)dx\end{array}$$
が成り立つことを「超関数 $f(x)$ と $g(x)$ が等しい」と定義することにします。つまり $f(x)$ と $g(x)$ の各点での値は必ずしも一致しません（つまりグラフが重なりません）が、全区間で積分した値が同じであれば、それを $f(x)=g(x)$ と書くことにします。

ディラックのデルタ関数

デルタ関数はイギリスの物理学者 P.A.M.Dirac によって考案された関数です。図のように $x$ 軸上に原点を中心として $2m$ の幅の中に物質が密度 $1/2m$ で分布しているような状況を考えます。
 

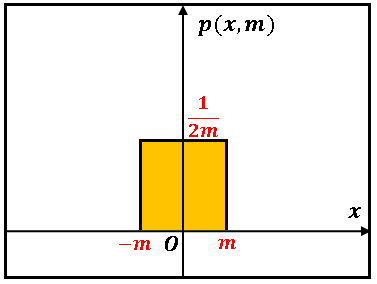
この分布関数 $p(x,m)$ は
 $$p(x,m)=\{\begin{array}{ll}\frac{1}{2m}& (-m\le x\le m)\\ 0& (x<-m,m<x)\end{array}$$
のように表すことができます。$p(x,m)$ を $x$ の全区間で積分すると
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p(x,m)dx={\int }_{-m}^m\frac{1}{2m}dx=1$$
となります（つまり総質量が 1 です）。この分布関数において $m$ をどんどん小さくしていくと下の図のように原点付近に圧縮された密度の高い状態となります。
 

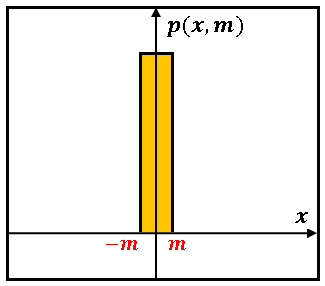
もちろん先ほどの積分計算の結果は同じですから総質量は 1 に保たれています。そして $m\to 0$ という極限を考えると
 $$\underset{m\to 0}{lim}p(x,m)=\{\begin{array}{ll}\mathrm{\infty }& (x=0)\\ 0& (x\ne 0)\end{array}$$
という関数が現れます。このような特異な関数をデルタ関数とよび、$\delta (x)$ と書きます。デルタ関数を正確に図に表すことはできませんが、限りなく細長くしたような棒線をイメージしてください。ここまでをまとめると、デルタ関数は
 $$\begin{array}{}\text{(C)}& \delta (x)=\{\begin{array}{ll}\mathrm{\infty }& (x=0)\\ 0& (x\ne 0)\end{array}\end{array}$$$$\begin{array}{}\text{(D)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (x)dx=1\end{array}$$
といった性質をもつ関数です。ここで分布関数にテスト関数 $\varphi (x)$ をかけて全区間で積分してみます。
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)p(x,m)dx={\int }_{-m}^m\frac{\varphi (x)}{2m}dx$$
ここで積分の平均値の定理（面積を適当な高さの長方形に均すことができるという定理）によって、
 $${\int }_{-m}^m\frac{\varphi (x)}{2m}dx=\frac{\varphi (c)}{2m}2m=\varphi (c)$$
となるような $\varphi (c)$ が存在しています。$m\to 0$ の極限をとれば、明らかに $\varphi (c)\to \varphi (0)$ となります。すなわち
 $$\begin{array}{}\text{(E)}& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)\delta (x)dx=\varphi (0)\end{array}$$
となります。ここで改めて、デルタ関数は上式 (E) を満たすような関数であると定義します。

デルタ関数の基本公式についてまとめておきます。
 $$\begin{array}{}\text{(F)}& f(x)\delta (x)& =f(0)\delta (x)\text{(G)}& x\delta (x)& =0\text{(H)}& \delta (ax)& =\frac{\delta (x)}{\mid a\mid }\text{(I)}& \delta (-x)& =\delta (x)\end{array}$$
【基本公式[F]と[G]の証明】先に述べたように、超関数 $f(x)$ と $g(x)$ が等しいというのは、
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)f(x)dx={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)g(x)dx$$
が成り立つということです。そこで左辺 $f(x)\delta (x)$ に $\varphi (x)$ をかけて積分すると
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\{f(x)\delta (x)\}\varphi (x)dx={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (x)\{f(x)\varphi (x)\}dx$$
ここでデルタ関数の基本的な性質である
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (x)\varphi (x)dx=\varphi (0)$$
を用いると
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\{f(x)\delta (x)\}\varphi (x)dx=f(0)\varphi (0)$$
となります。また右辺 $f(0)\delta (x)$ にテスト関数 $\varphi (x)$ をかけて積分すると
 $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(0)\delta (x)\varphi (x)dx=f(0)\varphi (0)$$
となります。よって
 $$f(x)\delta (x)=f(0)\delta (x)$$
が証明されました。この公式で $f(x)=x$ とおけば
 $$x\delta (x)=0$$
は明らかです。$f(x)=x$ に限らず、$f(x)=x^2$ など、原点で 0 になる関数を $\delta (x)$ に掛ければ 0 になります。そうでなければ公式 [F] より $y$ 切片の値に $\delta (x)$ を乗じた関数が得られます。グラフを思い描いてみると、公式というより、ほとんど自明の事実です。
【基本公式[H]と[I]の証明】$\delta (ax)$ にテスト関数 $\varphi (x)$ をかけて積分します。$a>0$ のとき、$ax=t$ とおくと、
 $$\begin{array}{rl}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)\delta (ax)dx& =\frac{1}{a}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi \left(\frac{t}{a}\right)\delta (t)dt\\ & =\frac{\varphi (0)}{\mid a\mid }={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)\frac{\delta (x)}{\mid a\mid }dx\end{array}$$
$a<0$ のとき、$a=-b(b>0),ax=-bx=t$ とおくと、
 $$\begin{array}{rl}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)\delta (ax)dx& =\frac{1}{b}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (-\frac{t}{b})\delta (t)dt\\ & =\frac{\varphi (0)}{b}=\frac{\varphi (0)}{\mid a\mid }={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x)\frac{\delta (x)}{\mid a\mid }dx\end{array}$$
よって被積分関数同士を比較すると
 $$\delta (ax)=\frac{\delta (x)}{\mid a\mid }$$
が得られます。この公式で $a=-1$ とすると
 $$\delta (-x)=\delta (x)$$
すなわちデルタ関数が偶関数であることがわかります。