対数関数の微分と積分

この記事では、対数関数 $\log{x}$ の微分と積分ついて解説します。

対数関数の導関数

　対数関数の微分 については次のような公式が知られています。
 \[\begin{align*}&(\log{x})’=\frac{1}{x}\tag{1}\\&(\log{ax})’=\frac{1}{x} \tag{2}\\&(\log{|f(x)|})’=\frac{f'(x)}{f(x)}\tag{3}\\&(\log_a{x})’=\frac{1}{x\log{a}}\tag{4}\end{align*}\]
【(1)の証明】微分の定義にしたがって証明します。
 \[\begin{align*}(\log x)’&=\lim_{\Delta x\rightarrow 0}\frac{\log(x+\Delta x)}{\Delta x}\\[6pt]&=\lim_{\Delta x\rightarrow 0}\frac{1}{\Delta x}\log \left( \frac{x+\Delta x}{\Delta x}\right)\\[6pt]&=\lim_{\Delta x\rightarrow 0}\log\left( 1+\frac{\Delta x}{x}\right)^{\frac{x}{\Delta x}\frac{1}{x}}\end{align*}\]
ここで極限公式
 \[\lim_{h\rightarrow 0}(1+h)^{1/h}=e\]
において $h=\Delta x/x$ とおくと
 \[\lim_{\Delta x\rightarrow 0}\left( 1+\frac{\Delta x}{x} \right)^{\frac{x}{\Delta x}}=e\]
となるので、対数関数の微分公式
 \[(\log x)’=\log e^{1/x}=\frac{1}{x}\]
が導かれます。

【(2)の証明】$\log a$ は定数ですから微分の途中で消えます。
 \[(\log{ax})’=(\log{a}+\log{x})’=\frac{1}{x}\]
【(3)の証明】$y=\log{|f(x)|}$ とおくと
 \[\frac{dy}{dx}=\frac{dy}{df}\frac{df}{dx}=\frac{f'(x)}{f(x)}\]
【(4)の証明】底の変換公式を用います。
 \[(\log_ax)’=\left ( \frac{\log{x}}{\log{a}} \right )’=\frac{1}{x\: \log{a}}\]　
 
対数関数の微分を積分形式で書くと次のようになります。
 \[\begin{align*}&\int\frac{dx}{x}=\log{x}+C\tag{5}\\&\int\frac{f'(x)}{f(x)}dx=\log\:|f(x)|+C\tag{6}\end{align*}\]　
≫【Amazon】ニュートン式 超図解 最強に面白い!! 対数

対数微分法

ある種の関数の微分は両辺の対数をとってから微分すると簡単になることがあります。この方法を対数微分法といいます。例として $y=x^x\,(x\gt 0)$ の導関数を対数微分法を使って求めてみます。両辺の対数をとると、
 \[\log{y}=x\log{x}\]
公式 (1) と (3) を使って両辺を微分します。
 \[\frac{y^\prime}{y}=\log{x}+1\]
これを整理して $y=x^x$ を戻すと
 \[y^\prime=x^x(\log{x}+1)\]
となります。続けて二階微分を対数微分法で計算してみましょう。上式の対数をとると
 \[\log{y^\prime}=x\log{x}+\log{\log{x}+1}\]
両辺の対数をとると
 \[\frac{y^{\prime\prime}}{y^\prime}=\log{x}+x\cdot\frac{1}{x}+\frac{1/x}{\log{x}+1}\]
右辺を整理すると
 \[\frac{y^{\prime\prime}}{y^\prime}=\log{x}+1+\frac{1}{x(\log{x}+1)}\]
$y^\prime=x^x(\log{x}+1)$ を戻すと
 \[y^{\prime\prime}=x^{x}\left\{(\log{x}+1)^2+\frac{1}{x}\right\}\]
を得ます。

対数関数の積分

まずは部分積分の例題として有名な式です。
 \[\begin{align*}\int\log{x}dx=x\log{x}-x+C \tag{7}\\[6pt]\int\log\frac{1}{x}dx=x-\log x+C\tag{8}\end{align*}\]
【証明】証明には部分積分を用います。
 \[\begin{align*}\int 1\cdot\log xdx&=x\log x-\int x\cdot\frac{1}{x}dx=x\log x-x+C\\[6pt]\int\log\frac{1}{x}dx&=x\log \frac{1}{x}-\int x\frac{-1/x^2}{1/x}dx=-x\log{x}+x+C\\[6pt]\end{align*}\]
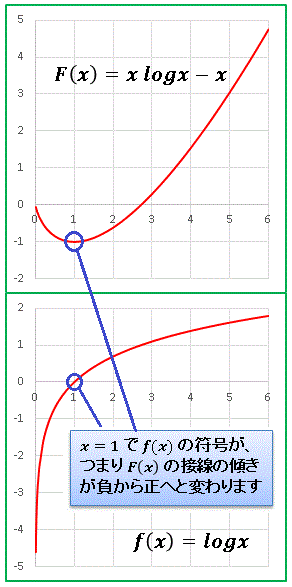
下図に $F(x) = x\log x-x$ および、その導関数である $f(x) = \log x$ を描いておきましたので、イメージを補強してください。
 

またとくに $1$ から $e$ までの定積分は
 \[\int_{1}^{e} \log{x}dx=1\tag{9}\]　
となるので、これも覚えておきましょう。計算例です：
 \[\int \log{(ax+b)}dx=\frac{1}{a}[(ax+b)\;\log{(ax+b)}-ax-b]+C\]
ちなみに上の計算には次の公式を用いています：
 \[\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C\]　
$\log{x}/x$ の積分もぜひ覚えておきたいところです。
 \[\int \frac{\log{x}}{x}dx=\frac{1}{2}(\log{x})^{2}+C\tag{10}\]
これは $dx/x=d(\log{x})$ と見れば自然と出てくる式です。