【Excel】誤差関数（ERF・ERF.PRECISE）

誤差関数と相補誤差関数

誤差関数は次のように定義される積分関数です。
\[\mathrm{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}\exp (-t^2)dt\tag{A}\]
誤差関数は正規分布と密接に関係しています。ここで
\[\mathrm{erf}\left(\frac{x}{\sqrt{2}\sigma}\right)=\frac{2}{\sqrt{\pi}}\int_{0}^{x/(\sqrt{2}\sigma)}\exp (-t^2)dt\]
において、
\[t=\frac{x}{\sqrt{2}\sigma}\]
のように変数変換してみると
\[\mathrm{erf}\left(\frac{x}{\sqrt{2}\sigma}\right)=\frac{2}{\sqrt{2\pi}\sigma}\int_{0}^{x}\exp\left(-\frac{x^2}{2\sigma^2}\right)dt\tag{A1}\]
となります。分散 $\sigma$ , 平均値 $\mu=0$ の正規分布確率密度は
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{x^2}{2\sigma^2}\right)\]
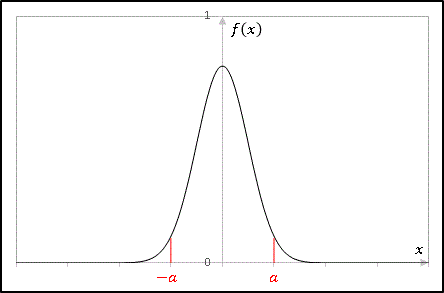
で与えられるので、(A1) はこの正規分布関数を $-x$ から $x$ まで積分した値に等しいことになります。ある測定値が正規分布で与えられる場合に、その測定値が $-a$ から $a$ の範囲にある確率は
\[P(a)=\mathrm{erf}\left(\frac{a}{\sqrt{2}\sigma}\right)\]
となるので、誤差関数という名前がついています。

相補誤差関数 は
\[\mathrm{erfc}(x)=\frac{2}{\sqrt{\pi}}\int_{x}^{\infty}\exp (-t^2)dt\tag{B}\]
と定義され、先程の議論から明らかに「測定値が $-a$ から $a$ の範囲にはない確率」が
\[\overline{P(a)}=\mathrm{erfc}\left(\frac{a}{\sqrt{2}\sigma}\right)\]
で与えられることを示しています。すなわち誤差関数との間に
\[\mathrm{erf}(x)+\mathrm{erfc}(x)=1\]
という関係が成り立ちます（確率の総和が 1 です）。

【Excel】ERF関数・ERF.PRECISE関数

Excel には誤差関数を計算するために ERF関数 と ERF.PRECISE関数 が用意されています。この関数は機能がよく似ていますが、若干異なっている部分があります。ERF.PRECISE関数は

=ERF.PRECISE(上限値)

というように、誤差関数の定義式
\[\mathrm{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}\exp (-t^2)dt\]
における積分の上限値 $x$ を引数に指定します。一方、ERF関数は

=ERF(下限値 [,上限値])

のような形で引数を指定します。たとえば

=ERF(1,5)

と入力すると
\[\frac{2}{\sqrt{\pi}}\int_{1}^{5}\exp (-t^2)dt\]
という積分を計算して 0.157 という値を返します。少しややこしいのですが、２つめの引数を省略すると指定した引数を上限値 $x$ とみなして
\[\frac{2}{\sqrt{\pi}}\int_{0}^{x}\exp (-t^2)dt\]
を計算することになります。たとえば

=ERF(2)

と入力すると
\[\frac{2}{\sqrt{\pi}}\int_{0}^{2}\exp (-t^2)dt\]
を計算して 0.995 という値を返します。

【Excel】ERFC関数・ERFC.PRECISE関数

ERFC関数 はセルに

=ERFC(x)

の形で入力して相補誤差関数
\[\mathrm{erfc}(x)=\frac{2}{\sqrt{\pi}}\int_{x}^{\infty}\exp (-t^2)dt\]
を計算します。また、ERFC.PRECISE関数 も

=ERFC.PRECISE(x)

と入力して相補誤差関数します。たとえば

=ERFC.PRECISE(1)

と入力すると
\[\mathrm{erfc}(x)=\frac{2}{\sqrt{\pi}}\int_{1}^{\infty}\exp (-t^2)dt\]
を計算して 0.157 という値を返します。

【Excel】誤差関数と相補誤差関数のグラフ

ERF関数 と ERFC関数を用いて $-6\leq x\leq 6$ の範囲で誤差関数と相補誤差関数の値を計算させてグラフを描くと次のようになります。



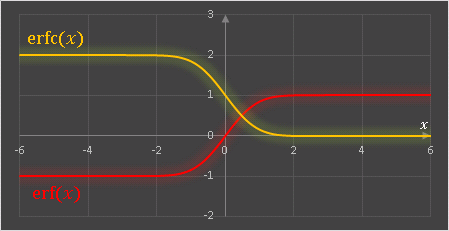
グラフからも $\mathrm{erf}(x)+\mathrm{erfc}(x)=1$ という関係が成り立っていることがわかります。