フェルマーの小定理

フェルマーの小定理

　$7$ を法とする整数 $a$ のベキ乗、すなわち
　
\[a^k\equiv x\quad (\mathrm{mod}\:7)\]
なる $x$ を計算して表に並べてみます。

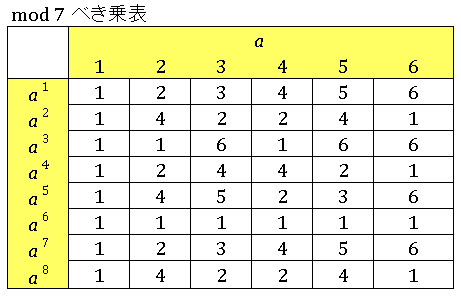
　$k$ が $6$ のところで $1$ が揃っています。つまり
　
\[a^6\equiv 1\quad (\mathrm{mod}\:7)\]
が成り立っているということです。前回学んだ オイラーの定理
　
\[(a,\:m)=1\quad\Longrightarrow\quad a^{\varphi(m)}\equiv 1\quad (\mathrm{mod}\:m)\]
において $m$ を素数 $p$ とすると $\varphi(p)=p-1$ なので以下の フェルマーの小定理 (Fermat’s little theorem) が成り立ちます。

　つまりフェルマーの小定理はオイラーの定理の特別な場合 ($m$ が素数である場合) に成り立つ定理です。普通であれば、フェルマーの小定理を先に証明して、その拡張としてオイラーの定理を説明するのですが、本講座では逆になってしまいました。まあ、証明の二度手間を省けたのでよしとしましょう。

　フェルマーの小定理を使えば、上の表にある通り
　
\[1^6\equiv 2^6\equiv 3^6\equiv \cdots\equiv 1\quad (\mathrm{mod}\:7)\]
が成り立つことがわかります。

フェルマーの大定理

　「フェルマーの小定理」というぐらいですから、もちろん「大定理」もあります。それは、かの有名な

という「フェルマーの大定理（最終定理）」です。17 世紀にフランスの数学者ピエール・ド・フェルマー (Pierre de Fermat) がディオファントスの著作『算術』の余白に「驚くべき証明法を発見したが余白が狭すぎて書けない」と書き残し、以後 360 年間もの長きにわたって大数学者たちがこの難題に挑みましたが、ことごとく敗れ去りました。しかし 1994 年にイギリスの数学者アンドリュー・ワイルズ (Andrew John Wiles) によって完全に証明されたので、以降は「ワイルズの定理」または「フェルマー・ワイルズの定理」ともよばれるようになりました。