位数（order）

新しい章に入りました。今回からは位数や原始根について調べていきます。

位数の定義

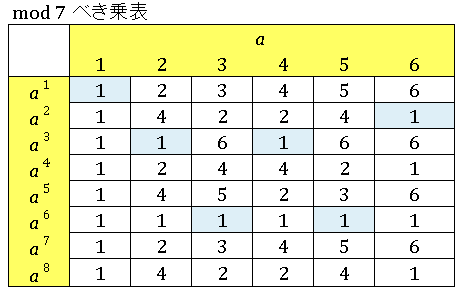
$a^k$ を $7$ で割ったときの余りを並べた表を再掲します。



フェルマーの小定理によれば、
\[a^6\equiv 1\quad (\mathrm{mod}\:7)\]
が成り立ちます（表では $1$ が並んでいます）が、もちろんそれ以外にも
\[a^k\equiv 1\quad (\mathrm{mod}\:7)\]
になるような数 $a^k$ はあります。表で青く塗ってあるところが、それぞれの $a$ について最小のベキ指数 $k$ で $a^k\equiv 1$ をみたす数字です。たとえば $a=2$ の場合は $k=3$ のとき合同式
\[2^3=8\equiv 1\quad (\mathrm{mod}\:7)\]
を満たし、かつ $k=3$ はこの合同式を成り立たせる最小のベキ指数です。そこで位数（order）というものを次のように定義します。

法 $7$ についての位数を表から読み取ると
\[\begin{align*}&\,\mathrm{ord}_7(1)=1\\[6pt]&\,\mathrm{ord}_7(2)=3\\[6pt]&\,\mathrm{ord}_7(3)=6\\[6pt]&\,\mathrm{ord}_7(4)=3\\[6pt]&\,\mathrm{ord}_7(5)=6\\[6pt]&\,\mathrm{ord}_7(6)=2\\[6pt]\end{align*}\]
となります。

位数の基本定理

たとえば $a=4$ のとき $\mathrm{ord}_7(4)=3$ で
\[4^3\equiv 1\quad (\mathrm{mod}\:7)\]
が成り立っています。以前に学んだ合同式ベキ乗に関する基本定理によると、
\[a\equiv b\quad (\mathrm{mod}\:m)\]
であれば
\[a^n\equiv b^n\quad (\mathrm{mod}\:m)\]
が成り立つので、
\[4^3\equiv 1\quad (\mathrm{mod}\:7)\]
についても両辺を $n$ 乗して

\[4^{3n}\equiv 1\quad (\mathrm{mod}\:7)\]
が成り立ちます。すなわち

\[4^3\equiv 4^6\equiv 4^9\equiv \cdots\equiv 1\quad (\mathrm{mod}\:7)\]
という合同式が成り立ちます。したがって
\[4^k\equiv 1\quad (\mathrm{mod}\:7)\]
という合同式が成り立たせる $k$ について

\[\mathrm{ord}_7(4)=3\,|\,k\]
が成り立つのではないかと予測できます。この段階では確証でなく予測にすぎないのは、上の議論ではたとえば $4^6$ と $4^9$ の間に $1$ と合同になる数がないとは断定できない（つまり別の周期で $1$ と合同になる数列の存在を否定できない）ので、以下の定理を証明しておく必要があります。

[証明] $\mathrm{ord}_m(a)=e$ とし、
\[k=eq+r\;(0\leq r\lt e)\]
とおきます。
\[1\equiv a^k\equiv a^{eq+r}\equiv (a^e)^q\,a^r\quad (\mathrm{mod}\:m)\]
$a^e\equiv 1\;\Leftrightarrow\; (a^e)^q\equiv 1\; (\mathrm{mod}\:m)$ なので
\[a^r\equiv 1\quad (\mathrm{mod}\:m)\]
$r\lt e$ なので、$r\neq 0$ とすると 位数 $e$ より小さな正数が上の合同式を満たすことになって矛盾します。よって $r=0$ となります。すなわち $k$ は $\mathrm{ord}_m(a)$ で割り切れます。（証明終）

特に $m$ が素数 $p$ のときは、フェルマーの小定理によって
\[a^{\,p-1}\equiv 1\quad (\mathrm{mod}\:p)\]
が成り立つので

となります。再び $\mathrm{mod}\:7$ の位数を並べてみます。
\[\begin{align*}&\,\mathrm{ord}_7(1)=1\\[6pt]&\,\mathrm{ord}_7(2)=3\\[6pt]&\,\mathrm{ord}_7(3)=6\\[6pt]&\,\mathrm{ord}_7(4)=3\\[6pt]&\,\mathrm{ord}_7(5)=6\\[6pt]&\,\mathrm{ord}_7(6)=2\\[6pt]\end{align*}\]
位数はすべて $p-1=7-1=6$ の約数になっています。

$p$ を法とする互いに合同でない集合

$a^k$ を $7$ で割ったときの余りを並べてみます。



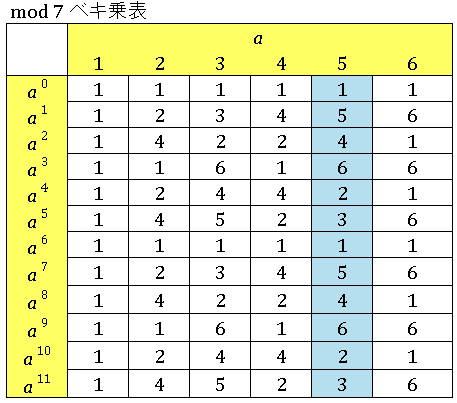
たとえば $a=5$ の列に着目すると、$7$ で割ったときの余りは

のように周期 $\mathrm{ord}_7(5)=6$ で並んでいます。つまり
\[5^0,\;5^1,\;5^2,\;5^3,\;5^4,\;5^5\]
は互いに合同ではなく、もし
\[5^m\equiv 5^n\quad (\mathrm{mod}\:7)\]
が成り立つのであれば、その周期から
\[m\equiv n\quad (\mathrm{mod}\:6)\]
が成り立ちます。たとえば
\[5^3\equiv 5^9\quad (\mathrm{mod}\:7)\]
が成り立っているので、
　
\[3\equiv 9\quad (\mathrm{mod}\:6)\]
が成り立つということです。これを一般的に述べたのが次の定理です。

[証明]
$a^0,\;a^1,\;a^2,\;\cdots,\;a^{e-1}$ のなかに互いに合同な要素があったとして、それを
\[a^s\equiv a^t\;(\mathrm{mod}\:p)\quad (0\leq s\lt t\lt e)\]
とおくと、
\[a^{t-s}\equiv 1\;(\mathrm{mod}\:p)\quad (0\lt t-s\lt e)\]
となり、これは $e$ の最小性に反します。よって
\[a^0,\;a^1,\;a^2,\;\cdots,\;a^{e-1}\]
は互いに合同ではないことが示されました。また
\[m=e\,q_1+r_1\quad (0\leq r_1\lt e)\]
とおくと、$a^e\equiv 1\;(\mathrm{mod}\:p)$ より
\[a^m=a^{e\,q_1+r_1}=(a^e)^{q_1}a^{r_1}\equiv a^{r_1}\;(\mathrm{mod}\:p)\]
となります。同様に
\[n=e\,q_2+r_2\quad (0\leq r_2\lt e)\]
とおくと、$a^n\equiv a^{r_2}\;(\mathrm{mod}\:p)$ なので
\[a^m\equiv a^n\;(\mathrm{mod}\:p)\]
が成り立つときは
\[a^{r_1}\equiv a^{r_2}\;(\mathrm{mod}\:p)\]
も成り立つことになります。$r_1,\;r_2$ は
\[0\leq r_1\lt e,\quad 0\leq r_2\lt e\]
すなわち、ともに位数 $e$ より小さい数なので、$a^{r_1}$ と $a^{r_2}$ が合同になるのは $r_1=r_2$ のときだけです。つまり $m$ と $n$ は $e$ で割ると余りが同じなので
\[m\equiv n\quad (\mathrm{mod}\:e)\]
が成り立ちます。（証明終）

x^k≡1(mod p)の根の個数

素数 $p$ を法とする $k$ 次合同方程式
\[x^k\equiv 1\quad (\mathrm{mod}\:p)\]
の根が最大でいくつあるのかを述べたのが次の定理です。

[証明]
数学的帰納法で証明します。$k=1$ のときは
\[x\equiv 1\quad (\mathrm{mod}\:p)\]
なので、これは1 元 1 次合同方程式で $(1,\:p)=1$ なので解は 1 つです。次に $k-1\;(k\geq 2)$ のときに根の個数が $k-1$ を超えないと仮定します。このとき合同方程式
\[x^k\equiv 1\quad (\mathrm{mod}\:p)\]
に根が１つもないならば定理は成り立っています。もし根が１つでもあって、それを $x_1$ とすれば
\[x_1^k\equiv 1\quad (\mathrm{mod}\:p)\]
が成り立ちます。よって
\[x^k-x_1^k\equiv 0\quad (\mathrm{mod}\:p)\]
左辺は $x=x_1$ を因数にもつので、$k-1$ 次式 $g(x)$ を用いて
\[x^k-x_1^k=(x-x_1)\,g(x)\]
と書くことができます。したがって
\[(x-x_1)\,g(x)\equiv 0\quad (\mathrm{mod}\:p)\]
$x_1$ と合同でない根を $x_2$ とすると
\[(x_2-x_1)\,g(x)\equiv 0\quad (\mathrm{mod}\:p)\]
$x_2-x_1\not\equiv 0,\:\:(x_2-x_1,p)=1$ なので
\[g(x_2)\equiv 0\quad (\mathrm{mod}\:p)\]
すなわち $x_2$ は $k-1$ 次合同方程式の解であり、仮定によりその根の個数は $k-1$ 個を超えません。したがって、
\[x^k\equiv 1\quad (\mathrm{mod}\:p)\]
の根の個数は $k$ 個を超えないことになります。（証明終）

法が素数ならば、$x^2\equiv 1$ の根は 2 個以内、$x^3\equiv 1$ の解は 3 個以内ということです。これを $n$ 次合同方程式の場合に一般化した定理はラグランジュの定理とよばれますが、それについてはもう少し先で紹介します。

合同計算の復習も兼ねて、$7$ を法とする $3^4$ の位数を求めてみます。
\[3^4\equiv 4\quad (\mathrm{mod}\:7)\tag{1}\]
はすぐにわかるので、両辺を 2 乗して
\[(3^4)^2\equiv 16\quad (\mathrm{mod}\:7)\]
$16\equiv 2\;(\mathrm{mod}\:7)$ なので
\[(3^4)^2\equiv 2\quad (\mathrm{mod}\:7)\tag{2}\]
(1) と (2) を辺々掛けて
\[(3^4)^3\equiv 8\equiv 1\quad (\mathrm{mod}\:7)\]
となるので、$3^4$ は 3 乗して初めて $1$ と合同になることがわかります。よって $3^4$ の位数は
\[\mathrm{ord}_7(3^4)=3\]
となります。

上の例では比較的簡単に位数を求めることができましたが、場合によってはなかなか $1$ と合同にならないこともあります。また、あまり大きな $a$ の位数は位数表にも載っていません。そこで $a$ の位数を用いて $a^k$ の位数を計算する公式を導いておきます。

[証明] $e=\mathrm{ord}_p(a^k),\:\:f=(d,\:k)$ とすると
\[d=fd’,\:\:k=fk’\]
のように書けて
\[(d’,\:k’)=1\]
となります。$e=\mathrm{ord}_p(a^k)$ より
\[a^{ke}\equiv 1\quad (\mathrm{mod}\:p)\]
が成り立つので
\[d\:|\:ke\quad\Longleftrightarrow\quad fd’\:|\:efk’\quad\Longleftrightarrow\quad d’\:|\:ek’\]
$(d’,\:k’)=1$ より $d’\:|\:e$ となります。
また、$d=fd’,\:\:k=fk’$ より $dk’=kd’$ なので
\[(a^k)^{d’}=(a^d)^{k’}\equiv 1\quad (\mathrm{mod}\:p)\]
$e=\mathrm{ord}_p(a^k)$ なので $e\:|\:d’$ となります。
$d’\:|\:e$ かつ $e\:|\:d’$ なので、
\[e=d’=\frac{d}{f}=\frac{d}{(d,\:k)}=\frac{\mathrm{ord}_p(a)}{(\mathrm{ord}_p(a),\:k)}\]
が成立します。（証明終）

位数表 などから $\mathrm{ord}_7(3)=6$ を既知として、冒頭で計算した $\mathrm{ord}_7(3^4)$ を定理 E4 を用いて計算してみると
\[\mathrm{ord}_7(3^4)=\frac{\mathrm{ord}_7(3)}{(\mathrm{ord}_7(3),\:4)}=\frac{6}{2}=3\]
となります。

p-1の約数に等しい位数は必ず存在する

いつものように素数 $\mathrm{mod}\:7$ のベキ乗表です。



$7-1=6$ の約数は $1,\;2,\;3,\;6$ ですが、表を見ると、それぞれの約数に等しい位数が存在していることがわかります。すなわち法 $7$ において、最小べき指数で $1$ と合同になる $a$ を分類してみると

のようになります。また個数については、オイラー関数で $\varphi(d)$ 個のように表されていますが、これは偶然ではないことが以下の定理によって示されます。

[証明] 位数 $d$ である数 $a$ が存在すると仮定します。
\[\mathrm{ord}_p(a)=d\]
すなわち $a$ のべきをつくっていくと
\[\{\:a^0,\;a^1,\;a^2,\;\cdots,\;a^k,\;\cdots,\;a^{d-1},\;a^d\:\}\]
となって $a^d$ のときに初めて $1$ と合同になります。ところが
\[\{\:a^0,\;a^1,\;a^2,\;\cdots,\;a^k,\;\cdots,\;a^{d-1}\:\}\tag{1}\]
もすべて $d$ 乗すると
\[(a^k)^d=(a^d)^k\equiv 1\quad (\mathrm{mod}\:p)\]
となるので、これらは位数 $d$ の候補です ($d$ が 1 と合同になる最小のべき指数とは限りません)。もちろん仮定によって $a$ の位数は $d$ ですが、他にもあるかもしれないということです。また (1) は定理 E2より法 $p$ に関して互いに合同ではありません。さらに (1) は合同方程式
\[x^d\equiv 1\quad (\mathrm{mod}\:p)\]
の根となっています。この合同方程式の解の個数は d 個を超えないので、(1) 以外に $d$ 乗して $1$ と合同になる数はありません。(1) の各要素の位数は定理 E4 より、
\[\mathrm{ord}_p(a^k)=\frac{\mathrm{ord}_p(a)}{(\mathrm{ord}_p(a),\:k)}=\frac{d}{(d,\:k)}\]
なので、位数が $d$ となるのは
\[(d,\:k)=1\]
を満たす $k$ に対応する $a^k$ だけです。
\[(d,\:1),\;(d,\:2),\:\cdots,\:(d,\,d-1)\]
の中から $1$ となるものだけを抜き出すので、その個数はオイラーの関数を用いて $\varphi (d)$ で表されます。ここまでの議論で
\[\mathrm{ord}_p(a)=d\]
を満たす $a$ があると仮定してきましたが、もしかすると存在しないかもしれません。そこで $p$ を法として位数 $d$ である数の個数を $\psi(d)$ とすると、

のどちらかです。これは $p-1$ の約数を $d_1,\;d_2,\;d_3,\;\cdots$ とすれば、たとえば
\[\begin{align*}&\psi(d_1)=\varphi(d_2)\\[6pt]&\psi(d_2)=0\\[6pt]
&\psi(d_3)=\varphi(d_3)\\[6pt]&\cdots\cdots\cdots\cdots\cdots\end{align*}\]
のように、約数によって、その約数に等しい位数があったりなかったりするかもしれないということです。しかし $\mathrm{ord}_p(a)\:|\:p-1$ より、$1$ から $p-1$ までの数はそれぞれが $p-1$ の約数のうちいずれかを位数とするので、
\[\sum_{d|p-1}\psi(d)=p-1\]
が成り立っているはずです。またオイラーの関数についても
\[\sum_{d|p-1}\varphi(d)=p-1\]
が成り立ちます。もしある $d$ について $\psi(d)=0$ であれば
\[\sum_{d|p-1}\psi(d)\lt\sum_{d|p-1}\varphi(d)\]
となってしまうので不合理です。よって任意の正の約数 $d$ に等しい位数をもつ整数 $a$ は必ず存在し、その個数は $\varphi(d)$ です。（証明終）