この記事では、VBA を用いてフレネル積分を計算し、そのデータをもとに、Excel のワークシートでグラフを描画します。
フレネル積分
フレネル正弦積分およびフレネル余弦積分は次のように定義されます。
\[\begin{align*}\mathrm{S}\,(x)=\int_{0}^{x}\sin^2tdt\\[6pt]\mathrm{C}\,(x)=\int_{0}^{x}\cos^2tdt\end{align*}\tag{A}\]
あるいは次のように定義される場合もあります。
\[\begin{align*}\mathrm{S}\,(x)=\int_{0}^{x}\sin\frac{\pi t^2}{2}dt\\[6pt]\mathrm{C}\,(x)=\int_{0}^{x}\cos\frac{\pi t^2}{2}dt\end{align*}\tag{B}\]
これらをまとめてフレネル積分(Fresnel integrals)とよびます。
シンプソンの公式を用いてフレネル積分を計算するユーザー定義関数を実装します。
'[VBA]フレネル正弦積分 Function FRESNEL_S(x As Double, Optional t As Boolean = False) As Double Dim p As Double, q As Double, r As Double Dim h As Double, s As Double, d As Double Dim m As Integer, k As Integer m = 256 h = x / (2 * m) d = 2 * Atn(1) s = 0 If t = False Then For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Sin(p ^ 2) + 4 * Sin(q ^ 2) + Sin(r ^ 2) Next k Else For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Sin(d * p ^ 2) + 4 * Sin(d * q ^ 2) + Sin(d * r ^ 2) Next k End If FRESNEL_S = s * h / 3 End Function '[VBA]フレネル余弦積分 Function FRESNEL_C(x As Double, _ Optional t As Boolean = False) As Double Dim p As Double, q As Double, r As Double Dim h As Double, s As Double, d As Double Dim m As Integer, k As Integer m = 256 h = x / (2 * m) d = 2 * Atn(1) s = 0 If t = False Then For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Cos(p ^ 2) + 4 * Cos(q ^ 2) + Cos(r ^ 2) Next k Else For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Cos(d * p ^ 2) + 4 * Cos(d * q ^ 2) + Cos(d * r ^ 2) Next k End If FRESNEL_C = s * h / 3 End Function
FRESNEL_S関数をワークシートで使用するときは
=FRESNEL_S(x[,関数の種類])
と入力します。[関数の種類] に False か 0 を指定する、あるいは省略すると定義式 (A) で計算します。True または 1 を指定すると定義式 (B) で計算します。FRESNEL_C関数をワークシートで使用するときは
=FRESNEL_C(x[,関数の種類])
と入力してください。[関数の種類] に False か 0 を指定する、あるいは省略すると定義式 (A) で計算します。True または 1 を指定すると定義式 (B) で計算します。この関数を使ってワークシートにグラフを描くと次のようになります。
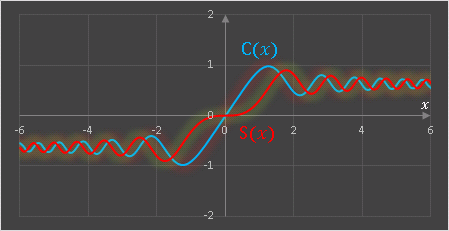
クロソイド(オイラーの螺旋)
$t$ を媒介変数とした $(x(t),\:y(t))=(C(t),\:S(t))$ は非常に美しい曲線を描きます。
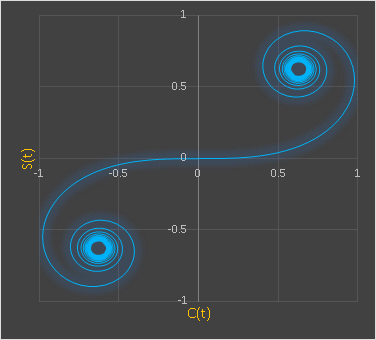
この曲線はクロソイドまたはオイラーの螺旋(オイラーのスパイラルとよばれています。もともと、この曲線は光学の回折現象などを幾何学的に表現するために用いられましたが、近年ではその曲率変化の特性を生かして、高速道路のカーブの設計にも応用されています。
より一般的に $\sin^nx$ と $\cos^n x$ の積分を計算するマクロも載せておきます。
'[VBA]sin^n(x)積分 Function ISN(x As Double, n As Integer) As Double Dim p As Double, q As Double, r As Double Dim h As Double, s As Double Dim m As Integer, k As Integer m = 512 h = x / (2 * m) s = 0 For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Sin(p ^ n) + 4 * Sin(q ^ n) + Sin(r ^ n) Next k ISN = s * h / 3 End Function '[VBA]cos^n(x) 積分 Function ICN(x As Double, n As Integer) As Double Dim p As Double, q As Double, r As Double Dim h As Double, s As Double Dim m As Integer, k As Integer m = 512 h = x / (2 * m) s = 0 For k = 0 To m - 1 p = 2 * k * h q = (2 * k + 1) * h r = (2 * k + 2) * h s = s + Cos(p ^ n) + 4 * Cos(q ^ n) + Cos(r ^ n) Next k ICN = s * h / 3 End Function
ISN関数をワークシートで使用するときは
=ISN(x,n)
ICN関数をワークシートで使用するときは
=ICN(x,n)
と入力します。x は任意の数値、n は整数を指定してください。この関数を用いて計算した $\sin^3x$ と $\cos^3x$ の 0 から $x$ までの積分は次のようなグラフになります。
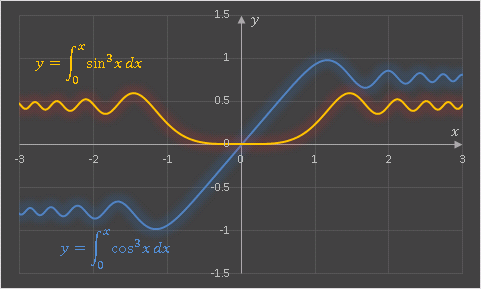
エクセルや数学に関するコメントをお寄せください