ここに 12 個の要素をもつ集合
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
があります。この集合の中に含まれる自然数と平方数は、どちらのほうが多いでしょうか？ そんなことは訊かれるまでもなく自然数に決まっていますね。上の集合から平方数だけを取り出して部分集合をつくってみると …
{1, 4, 9}
たった 3 つしかありません。「自然数を順に並べてつくった集合に含まれる自然数は平方数よりも多い」ということは常識のように思えますが …
ガリレオを怯ませた無限の深遠
ガリレオ・ガリレイ (Galileo Galilei) といえば、地動説を唱えてカトリック教会を敵に回し、異端審問所の厳しい追及を受けたというエピソードが有名な科学者ですね。望遠鏡を作って土星の輪や衛星を発見したり、振り子の等時性を発見したりと、どちらかといえば物理学者の印象が強い人物ですが、実は数学の分野でも大変重大な発見をしています。それはある意味「地動説」よりも深遠であり、それまで１千年以上停滞していた数学を飛躍させるきっかけともなる発見でした。
その発見は彼の著書『新科学対話』に記されています。
平方数は自然数全体と同じだけの数があると結論せざるをえない。
ここだけ読むとぎょっとするような文章ですが、ガリレオが扱っていたのは有限集合ではなく無限集合です。
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...}
と果てしなく続く自然数の集合においては、平方数は自然数と同じだけ存在すると主張しているのです。しかしそんなことがありえるでしょうか？ 自然数に比べると平方数は稀にしか出現しません。たとえ無限集合であっても、直感的には自然数のほうがずっと多いはずだと思ってしまいますね。しかしガリレオは、自然数と平方数に次のような対応関係をつけることで「同じだけ存在する」ことを説明しています。
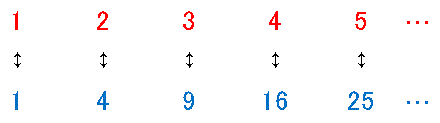
つまり 1 に対しては 1 を、2 に対しては 4 を … というように対応させていけば、どんな自然数に対しても必ず 1 つの平方数が割り振られていくのだから、この 2 種類の数は同じ数だけある、と結論したのです。もう少し一般的な言葉で言うと、
無限集合は自身よりも小さい部分集合と要素の数が等しくなりうる
という発見でした。これはとても重要な発見であり、有限集合と無限集合は決定的に異なるものであることを示唆しています。この発見は後のボルツァノ・ワイエルシュトラスの定理などの発見につながっていくのですが、ガリレオ自身は無限についてこれ以上踏み込むことをやめてしまいました。あれほど果敢に真実に挑んできたガリレオを怯ませるほどの底知れぬ何かが「無限」の中には潜んでいたのです。それはもしかすると異端審問所と対峙する以上の恐怖だったのかもしれません。
≫ アラビア数字の起源
エクセルや数学に関するコメントをお寄せください
【AI連載小説】数学のリズム、エクセルの旋律(36)
「無限集合の特異な性質について語ります」
真琴、研伸、月子の三人は、サークルの勉強会で無限集合の性質について討論していました。
真琴：「無限集合って面白いよな。例えば、自然数全体の集合を考えると、これは無限だけど、自然数の偶数の集合も無限だよね」
研伸：「でも、無限って言っても、どちらも無限ってことは同じなのかな？」
月子：「無限って概念が抽象的で難しいところだね。でも、無限集合同士で要素の数が等しいことがあるよ」
真琴：「それってどういうこと？」
月子：「例えば、自然数全体の集合Nとその偶数の集合Eを考える。自然数は無限だし、偶数も無限だけど、どちらも要素の数は同じだと言えるよ」
研伸：「それは不思議だな。無限って言っても、要素の数に大小があるんだ」
月子：「これは無限集合の性質の一つで、カントールの対角線論法とかで証明されることもあるよ」
真琴：「無限って本当に奥が深いな。どんどん新しい発見があって面白い」
三人の討論は、無限集合の特異な性質について深く追求し、数学の不思議な世界に思索を巡らせていました。