【Excel】双曲線関数（COSH, SINH, TANH）

この記事で扱う Excel データは Hyperbolic.xlsx ファイルに入っています。
≫ Hyperbolicブックをダウンロード

双曲線関数

双曲線正弦関数（hyperbolic cosine）と双曲線余弦関数（hyperbolic sine）はそれぞれ双曲線 $X^2-Y^2=1$ 上の $X$ 座標および $Y$ 座標として定義されています。



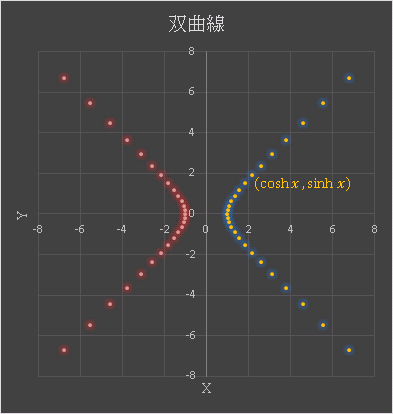
双曲線正弦関数と双曲線余弦関数は指数関数を用いて
　\[\begin{align*}X&=\cosh x=\frac{e^x+e^{-x}}{2} \tag{1}\\[6pt]Y&=\sinh x=\frac{e^x-e^{-x}}{2} \tag{2}\end{align*}\]
と表すことができます（この表式が正しいことは (1) と (2) を双曲線方程式 $X^2-Y^2=1$ に代入して確かめることができます）。また、双曲線正接関数（hyperbolic tangent）は次のように定義します。
\[\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}} \tag{3}\]
(1) から (3) をまとめて双曲線関数と呼びます。定義より明らかに
\[\cosh ^2x-\sinh ^2x=1 \tag{4}\]
が成り立っています。$\sinh x$ と $\tanh x$ は奇関数、 $\cosh x$ は偶関数です。グラフを描くと下図のようになります。

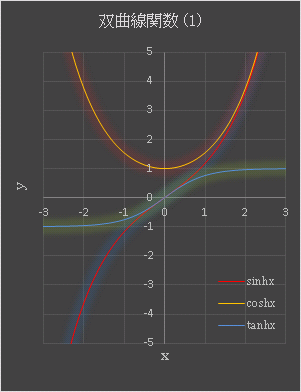
他にも双曲線正割 (hypabolic secant)、双曲線余割 (hypabolic cosecant)、双曲線余接 (hypabolic cotangent) とよばれる関数があって、それぞれ以下のように定義されています。
\[\begin{align*}\mathrm{sech}x&=\frac{1}{\mathrm{cosh}x}=\frac{2}{e^x+e^{-x}}\tag{5}\\[6pt]\mathrm{csch}x&=\frac{1}{\mathrm{sinh}x}=\frac{2}{e^x-e^{-x}}\tag{6}\\[6pt]\mathrm{coth}x&=\frac{\mathrm{cosh}x}{\mathrm{sinh}x}=\frac{e^{2x}+1}{e^{2x}-1}\tag{7}\end{align*}\]
三角関数の $\cos x$ と $\sin x$ が単位円上の点であるのに対し、双曲線関数の $\cosh x$ と $\sinh x$ は双曲線上の点です。双曲線関数の公式群は三角関数の公式ととてもよく似ています。以下に双曲線関数の基本公式一覧を載せておきます。
\[\begin{align*}&\sinh (x \pm y) = \sinh x\cosh y \pm \cosh x\sinh y \tag{8}\\[6pt]&\cosh (x \pm y) = \cosh x\cosh y \pm \sinh x\sinh y \tag{9}\\[6pt]&\tanh (x \pm y) = \frac{\tanh x \pm \tanh y}{1 \pm \tanh x\tanh y} \tag{10}\\[6pt]\\[6pt]&\sinh 2x=2\sinh x\cosh x \tag{11}\\[6pt]&\cosh 2x=2\cosh ^2x-1=1+2\sinh ^2x \tag{12}\\[6pt]\\[6pt]&\sinh x+\sinh y=2\sinh \frac{x+y}{2} \cosh \frac{x-y}{2} \tag{13}\\[6pt]&\sinh x-\sinh y=2\sinh \frac{x-y}{2} \cosh \frac{x+y}{2} \tag{14}\\[6pt]&\cosh x+\cosh y=2\cosh \frac{x+y}{2} \cosh \frac{x-y}{2} \tag{15}\\[6pt]&\cosh x-\cosh y=2\sinh \frac{x+y}{2} \sinh \frac{x-y}{2} \tag{16}\\[6pt]\\[6pt]&2\sinh x\sinh y=\cosh (x+y)-\cosh (x-y)\tag{17}\\[6pt]&2\sinh x\cosh y=\sinh (x+y)-\sinh (x-y)\tag{18}\\[6pt]&2\cosh x\sinh y=\sinh (x+y)-\sinh (x-y)\tag{19}\\[6pt]&2\cosh x\cosh y=\cosh (x+y)-\cosh (x-y)\tag{20}\end{align*}\]

双曲線関数の微分積分

双曲線関数の微分公式も三角関数の微分公式とよく似ています。$\sinh x$ と $\cosh x$ は互いに導関数となっています。
\[\begin{align*}(\sinh ax)’&=a\cosh ax \tag{21}\\[6pt](\cosh ax)’&=a\sinh ax \tag{22}\\[6pt](\tanh ax)’&=\frac{a}{\cosh ^2ax} \tag{23}\\[6pt]\int \cosh axdx&=\frac{1}{a}\sinh ax \tag{24}\\[6pt]\int \sinh axdx&=\frac{1}{a}\cosh ax \tag{25}\\[6pt]\int \tanh axdx&=\frac{1}{a}\log (\cosh ax) \tag{26}\end{align*}\]

Excelの双曲線関数

Excel で双曲線正弦 ($\sinh x$)、双曲線余弦 ($\cosh x$)、双曲線正接 ($\tanh x$) を計算するときには、それぞれ SINH, COSH, TANH を使います。たとえば

=SINH(0)

とすれば $\sinh 0$ の値「0」が返ります。任意の $x$ について
\[\cosh ^2x-\sinh ^2x=1\]
が成り立っていることを Excel で確認してみましょう。ダウンロードした Hyperbolic ブックの plot_3 シートには、区間 $[-5,\ 5]$ の範囲で $\cosh ^2x-\sinh ^2x$ を計算しています (下図)。

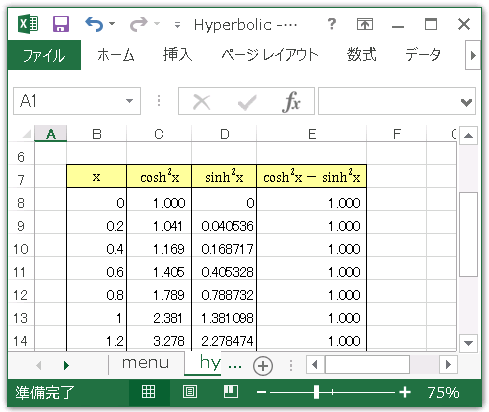
すべて値が $1$ になっていることが確認できます。このように、$\cosh x$ と $\sinh x$ は双曲線上の点として定義されているので、媒介変数 $t$ に適当な範囲の値を与えて、$\cosh t$ および $-\cosh t$ に対して $\sinh t$ の値をプロットすると、双曲線が描かれます。このグラフのデータは plot_0 シートにあります (下図)。

plot_1 シートには、変数 $x$ に対する双曲線関数 $\sinh x,\ \cosh x,\ \tanh x$ のグラフの概形が載っています (下図)。



双曲線正弦関数 $\sinh x$ は $x \to \infty$ では $e^{-x}$ が $0$ になるので、漸近線一つは $y=e^x/2$ です。また逆に $x \to -\infty$ では $e^{x}$ が $0$ になるので、もう一つ漸近線は $y=-e^{-x}/2$ です。同様に考えて、$\cosh x$ の漸近線は $e^{x}/2$ と $e^{-x}/2$ です。$\sinh x$ と $\tanh x$ は奇関数、$\cosh x$ は偶関数です。

漸近線を考慮すると、十分大きな正の $x$ に対して、$\sinh x$ と $\cosh x$ は、ほとんど同じ値をとります。しかし、$\cosh^2 x$ と $\sinh^2 x$ については、$x$ がどれほど大きくなっても常にその差 $1$ をキープします。この事実は直感に反していますが、極限操作ではこのようなことが、しばしば起こります。

Excel で双曲線正割 ($\mathrm{sech}x$)、双曲線余割 ($\mathrm{csch} x$)、双曲線余接 ($\mathrm{coth} x$) を計算するときは、それぞれ SECH, CSCH, COTH を使います。たとえば

=SECH(0)

とすれば sech0 の値「1」が返ります。plot_2 シートには双曲線関数 $\mathrm{sech}x,\ \mathrm{csch}x,\ \mathrm{coth}x$ のグラフが載っています (下図)。

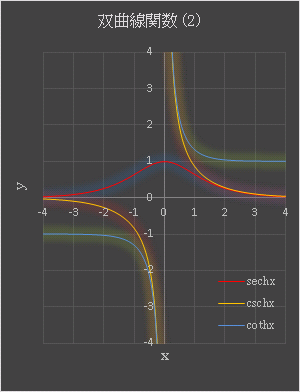
逆双曲線関数

逆双曲線関数（inverse hyperbolic functions）は双曲線関数の逆関数として定義されます。たとえば、双曲線正弦関数
\[y=\frac{e^x-e^{-x}}{2}\tag{27}\]
を $x$ について解いてみましょう。$e^x=t$ とおくと、
\[2y=t-\frac{1}{t}\tag{27}\]
となります。$t$ について整理すると
\[t^2-2yt-1=0\tag{27}\]
という $t$ の二次方程式が得られるので、これを解いて
\[t=y\pm\sqrt{y^2+1}\tag{30}\]
となります。変数を $t$ から $x$ に戻すと
\[e^x=y\pm\sqrt{y^2+1}\tag{31}\]
となるので、両辺の自然対数をとって
\[x=\log(y\pm\sqrt{y^2+1})\tag{32}\]
という表式を得ます。$x$ と $y$ を入れ替えると、
\[y=\log(x\pm\sqrt{x^2+1})\tag{33}\]
となります。このままでは二価関数となってしまうので、正符号を採用して、
\[y=\log(x+\sqrt{x^2+1})\tag{34}\]
を逆双曲線正弦関数と定義し、$\mathrm{arsinh}x$ という記号で表します。双曲線余弦と双曲線正接の逆関数も同様に定義して、それぞれ $\mathrm{arcosh}x,\ \mathrm{artanh}x$ で表します：
\[\begin{align*}\mathrm{arsinh}x&=\log (x+\sqrt{x^2+1})\tag{35}\\[6pt]\mathrm{arcosh}x&=\log (x+\sqrt{x^2-1}) \quad (1 \leq x)\tag{36}\\[6pt]\mathrm{artanh}x&=\frac{1}{2}\ \log \left( \frac{1+x}{1-x}\right)\quad (-1 \lt x \lt 1)\tag{37}\end{align*}\]
逆双曲線関数は双曲線 x y = 1 に対応する双曲的扇形の面積に等しいことから面積関数と呼ばれることもあります。arsinh の接頭辞 ar は area（面積）を意味しています。逆三角関数の接頭辞 arc と間違えやすいので注意が必要です。

実は数学の専門書でも arsinh が arcsinh となっていたりするなど、arc という書き方も一般的に定着してしまっているので完全に誤りであるとは言えませんが、国際標準化機構（ISO：the International Organization for Standardization）では双曲線逆正弦を arsinh と定めていて、Excel の英語版公式ホームページでも逆三角関数を

 ASIN：arcsine
 ACOS：arccosine
 ATAN：arctangent

と記述しているのに対して逆双曲線関数を

 ASINH：Inverse hyperbolic sine
 ACOSH：Inverse hyperbolic cosine
 ATANH：Inverse hyperbolic tangent

と書いて、読み方をきちんと分けています。

【Excel】逆双曲線関数

Excel では逆双曲線関数 $\mathrm{arsinh}x,\ \mathrm{arcosh}x,\ \mathrm{artanh}x$ をそれぞれ、ASINH, ACOSH, ATANH を使って計算します。たとえば

=ASINH(1)

とすれば、$\mathrm{arsinh}1$ を計算して 0.881 を返します。Hyperbolic ブックの plot_4 シートには逆双曲線関数のグラフがプロットされています。
 

 
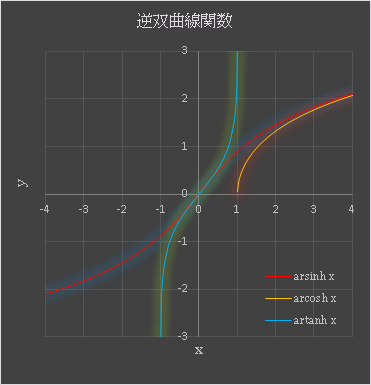
グラフからわかるように、$\mathrm{arsinh}x$ は全ての実数 $x$ で定義されていますが、$\mathrm{arcosh}x$ は $1 \leq x$, $\mathrm{artanh}x$ は $-1 \lt x \lt 1$ の範囲に限定される関数です。

双曲線余弦関数と二次関数のグラフの概形を眺めてみると、どちらも下に凸で左右対称なのではよく似ています。しかし、双曲線余弦関数は $x\to\pm\infty$ で指数関数 $e^{\pm x}/2$ として振る舞うので、はるかに増加率の大きな関数です。試しに、$\cosh x$ から $x^2+1$ を引いて
\[y=\cosh x-x^2-1\]
という関数をつくってグラフに描いてみました。

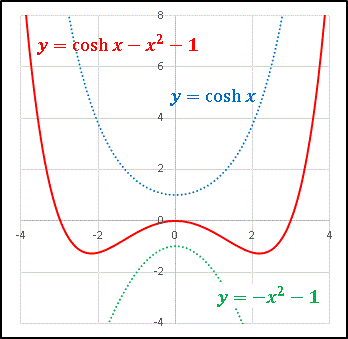
$y = \cosh x$ (青い点線) と $y=-x^2-1$ (緑の点線) の間を縫うような曲線となっています。先にも述べたように指数関数のほうが二次関数より増加率が大きいので、全体としては $x\to\pm\infty$ で発散する関数となっています。しかし、$|x|$ が小さい範囲では二次関数のほうが大きな値をとります。上のグラフを見ると、$-2\lt x\lt 2$ のあたりでは二次関数に引張られて一時的に値を落として極値を 2 つ作っています。

今度は双曲線余弦関数 $\cosh x$ を $x^2$ で割って
　\[y=\frac{\cosh x}{x^2}=\frac{e^x+e^{-x}}{2x^2} \qquad (0 \lt x)\]
という関数のグラフの概形を描いてみます。

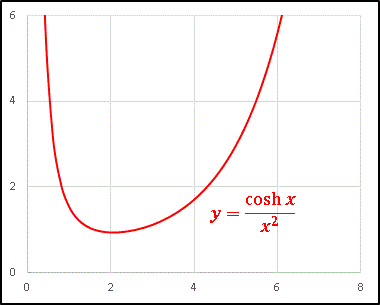
やはり双曲線余弦関数のほうが増加率が大きいので、$x\to\pm\infty$ で $\pm\infty$ に発散する関数となっています。最小値は $x=2$ のあたりにありそうです。Excel ばかり使わずに、たまには少し手を動かして確認しておきましょう。両辺に $x^2$ をかけて
\[2x^2y=e^x+e^{-x}\]
の両辺を微分すると
\[4xy+2x^2y’=e^x-e^{-x}\]
この式から $y’$ を求めると、
\[y’=\frac{e^x-e^{-x}}{2x^2}-\frac{4xy}{2x^2}=y-\frac{2y}{x}= y\left( 1-\frac{2}{x} \right)\]
となるので、$y’=0$ とおくと、ちょうど $x=2$ で最小値をとることがわかります。

【VBA】双曲線関数

VBA で双曲線関数を使いたいときは、ワークシート関数を呼び出すのが一番簡単です。値を変数に格納する場合はデータ型を倍精度実数型 (Double) で宣言しておきます。たとえば、サブルーチンの中で双曲線正弦関数を計算する場合は以下のようなコードを書きます。

'[VBA]双曲線正弦関数の計算
Sub Hyperbolic_Sine()
　　Dim x As Double
　　x = WorksheetFunction.Sinh(1)
　　Debug.Print x
End Sub

'実行結果：1.1752011936438

他には、Functionマクロとして VBA 独自の双曲線関数を定義する方法もあります。

'[VBA]Hyperbolic Sine
Function Sinh(x As Double) As Double
　　Sinh = (exp(x) - exp(-x)) / 2
End Function

'[VBA]Hyperbolic Cosine
Function Cosh(x As Double) As Double
　　Cosh = (exp(x) + exp(-x)) / 2
End Function

'[VBA]Hyperbolic Tangent
Function Tanh(x As Double) As Double
　　Tanh = Sinh(x) / Cosh(x)
End Function

'[VBA]独自定義した双曲線関数の動作テスト
Sub Hyperbolic_Test()
　　Debug.Print "Sinh(1) : " & Sinh(0)
　　Debug.Print "Cosh(1) : " & Cosh(1)
　　Debug.Print "Tanh(1) : " & Tanh(1)
End Sub

'実行結果：
Sinh(1) : 0
Cosh(1) : 1.54308063481524
Tanh(1) : 0.761594155955765