広義積分とコーシーの主値積分

この記事では、区間内に不連続点がある場合の積分、あるいは無限区間における積分について解説します。

広義積分

不連続な関数の積分

関数 $f(x)$ が $a<x\le b$ で連続であって、
 $$\underset{\epsilon \to +0}{lim}{\int }_{a+\epsilon }^{b}f(x)dx$$
が存在するとき、$f(x)$ は $a\le x\le b$ で積分可能であるといい、
 $${\int }_a^{b}f(x)dx=\underset{\epsilon \to +0}{lim}{\int }_{a+\epsilon }^{b}f(x)dx$$
と表します。同様に関数 $f(x)$ が $a\le x<b$ で連続で
 $$\underset{\epsilon \to +0}{lim}{\int }_a^{b-\epsilon }f(x)dx$$
が存在するとき、$f(x)$ は $a\le x\le b$ で積分可能であるといい、
 $${\int }_a^{b}f(x)dx=\underset{\epsilon \to +0}{lim}{\int }_a^{b-\epsilon }f(x)dx$$
と表します。また $f(x)$ が区間 $[a,b]$ 内の 1 点 $c$ を除いて連続である場合は、
 $$\underset{{\epsilon }_1\to +0}{lim}{\int }_a^{c-{\epsilon }_1}f(x)dx,\underset{{\epsilon }_2\to +0}{lim}{\int }_{c+{\epsilon }_2}^{b}f(x)dx$$
という極限値が存在する場合に限って、
 $${\int }_a^{b}f(x)dx=\underset{{\epsilon }_1\to +0}{lim}{\int }_a^{c-{\epsilon }_1}f(x)dx+\underset{{\epsilon }_2\to +0}{lim}{\int }_{c+{\epsilon }_2}^{b}f(x)dx$$
と定義します。

1/xの積分と1/√xの積分

関数 $y=1/x$ と $y=1/\sqrt{x}$ はともに $x=0$ で不連続となっています。$y=1/x$ については
 $$\underset{\epsilon \to +0}{lim}{\int }_{\epsilon }^1\frac{dx}{x}=\underset{\epsilon \to +0}{lim}[\log x{]}_{\epsilon }^1=\mathrm{\infty }$$
となって積分を定義することはできません。しかし $y=1/\sqrt{x}$ については
 $$\underset{\epsilon \to +0}{lim}{\int }_{\epsilon }^1\frac{dx}{\sqrt{x}}=\underset{\epsilon \to +0}{lim}[2\sqrt{x}{]}_{\epsilon }^1=2$$
と有限値をもつので、
 $${\int }_{\epsilon }^1\frac{dx}{\sqrt{x}}=2$$
とすることができます。$y=1/x$ と $y=1/\sqrt{x}$ のグラフを描いてこの違いを直感的に把握してみます。
 

 
ともに $x\to 0$ で ∞ となる関数ですが、曲線と $x$ 軸および $x=1$ で囲まれる面積を求めると $y=1/x$ の場合は値が無限大になり、$y=1/\sqrt{x}$ のときはは有限値となります。その理由は $y=1/\sqrt{x}$ は $x\to 0$ となるときに、$y$ 軸との間隔を十分に細くしていくからです。つまり縦幅が非常に大きくなっても、横幅がそれを相殺するように狭くなっているので、実のところ原点付近の面積はほんの僅かしかないということです。

無限区間積分

関数 $f(x)$ が $x\ge a$ で連続であり
 $$\underset{b\to +\mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
が存在するとき、
 $${\int }_a^{\mathrm{\infty }}f(x)dx=\underset{b\to +\mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
と定義します。また関数 $f(x)$ が $x\le b$ で連続であって
 $$\underset{a\to -\mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
が存在するとき、
 $${\int }_{-\mathrm{\infty }}^{b}f(x)dx=\underset{a\to -\mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
と定義します。さらに関数 $f(x)$ が全区間で連続であって
 $$\underset{a\to -\mathrm{\infty }}{lim}\underset{b\to \mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
が存在するとき、
 $${\int }_{-\mathrm{\infty }}^{-\mathrm{\infty }}f(x)dx=\underset{a\to -\mathrm{\infty }}{lim}\underset{b\to \mathrm{\infty }}{lim}{\int }_a^{b}f(x)dx$$
と定義します。

e^xを[-∞,0]で積分

次のような積分
 $${\int }_{-\mathrm{\infty }}^0{e}^{x}dx$$
を計算してみます。
 $$\underset{a\to -\mathrm{\infty }}{lim}{\int }_a^0{e}^{x}dx=\underset{a\to -\mathrm{\infty }}{lim}[e^x{]}_a^0=1$$
という極限値が存在しているので、
 $${\int }_{-\mathrm{\infty }}^0{e}^{x}dx=1$$
となります。

コーシーの主値積分

再び関数 $y=1/x$ について、今度は区間 $[-1,1]$ で考えてみます。
 

 
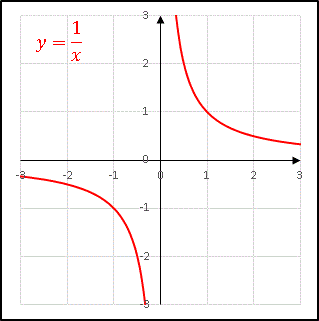
先ほどの広義積分の定義によると、
 $$\underset{{\epsilon }_1\to +0}{lim}{\int }_{-1}^{1-{\epsilon }_1}\frac{1}{x}dx,\underset{{\epsilon }_2\to +0}{lim}{\int }_{1+{\epsilon }_2}^1\frac{1}{x}dx$$
はいずれも有限値をもたないので、
 $${\int }_{-1}^1\frac{1}{x}dx$$
を計算することはできません。しかし上のグラフを見ると直感的に「この積分は正の面積と負の面積がキャンセルしあって 0 になるはずでは？」と考える人も多いでしょう。そこで ${\epsilon }_1={\epsilon }_2=\epsilon$ として
 $${\int }_a^{b}f(x)dx=\underset{\epsilon \to +0}{lim}\{{\int }_a^{c-\epsilon }f(x)dx+{\int }_{c+\epsilon }^{b}f(x)dx\}$$
という極限で積分を定義します。この極限値のことを コーシーの主値積分 (Cauchy’s principal value of integral) とよびます。すると
 $${\int }_{-1}^1\frac{1}{x}dx$$
もコーシーの主値積分は存在します。実際に計算してみると
 $$\begin{array}{rl}\underset{\epsilon \to +0}{lim}& \{{\int }_{-1}^{-\epsilon }\frac{1}{x}dx+{\int }_{\epsilon }^1\frac{1}{x}dx\}\\ & =\underset{\epsilon \to +0}{lim}\{-(\log 1-\log \epsilon )+(\log 1-\log \epsilon )\}=0\end{array}$$
となります。