【Excel】LCMで最小公倍数表を作成する

【Excel】LCM関数

Excel の LCM 関数は 2 つの数値を受け取って、最小公倍数を返します。たとえば

=LCM(8,12)

と入力すれば 8 と 12 の最小公倍数 24 を返します。LCM は Least Common Multiple の略です。LCM関数を用いると、普通の方法では計算の難しい大きな数の最小公倍数を計算できます。たとえば

=LCM(42,124)

と入力すれば 2604 を得られます。

最小公倍数計算シート

２つの数値を入力して最小公倍数を計算するシートをつくってみましょう。次の図を参照してください。
 

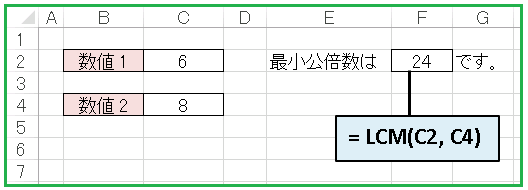
セル C2 とセル C4 には、ユーザーが好きな値を入力できるようにしておきます。
今はとりあえず 6, 8 を入れておきましょう。
F24 にはセル C2 とセル C4 を引数に指定して

=LCM(C2,C4)

と入力します。「24」が出力されるはずです。あとはセル C2 とセル C4 に好きな数字を入れて、色々と試してみてください。
 
また、２つの数字の公倍数はこの最小公倍数の倍数ですから、これもワークシートで簡単に計算させることができます。

最小公倍数表

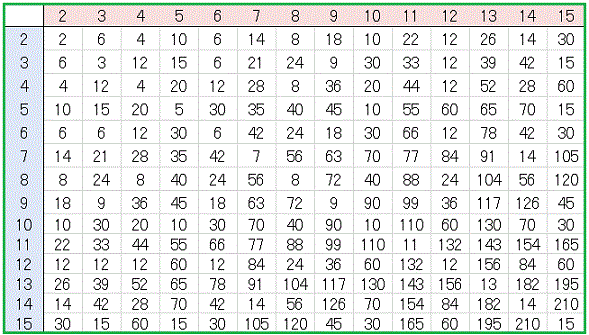
LCM 関数を使って 2 ～ 15 の最小公倍数表を作ってみました。必要であれば画像をコピーしてお持ち帰りください。
 

公倍数と最小公倍数

$3$ の倍数と $5$ の倍数を並べてみましょう。九九表の $3$ の列と $5$ の列です。
 \[\begin{align*}
&3,\ 6,\ 9,\ 12,\ 15,\ 21,\ 24,\ 27,\ 30,\ 33\:\cdots\\[6pt]
&5,\ 10,\ 15,\ 20,\ 25,\ 30,\ 35,\ 40,\ 45,\ 50\:\cdots\end{align*}\]
そして共通する数を [] で括ります。
 \[\begin{align*}
&3,\ 6,\ 9,\ 12,\ [15],\ 21,\ 24,\ 27,\ [30],\ 33,\:\cdots\\[6pt]
&5,\ 10,\ [15],\ 20,\ 25,\ [30],\ 35,\ 40,\ 45,\ 50\:\cdots\end{align*}\]
とりあえず、$15$ と $30$ という共通の数が見つかりましたね。これが公倍数とよばれる数です。もっとたくさんの数を並べていくと、このような数は無限に見つかります。公倍数の中で一番数の小さいものを最小公倍数とよびます。$3$ と $5$ の最小公倍数はもちろん $15$ ですね。これを記号で $\left\{3,5\right\}=15$ のように書くこともありますが、集合の $\left\{\right\}$ と勘違いされることもあるので、使い方には注意が必要です。

全ての公倍数は最小公倍数の倍数になっています。つまり $15$ の倍数を並べて
 \[15,\ 30,\ 45,\ 60,\ 75,\ 90,\:\cdots\]
これらの数が $3$ と $5$ の公倍数となっています。一見して当たり前のようにも思えますが、こんなに簡単なことでも全てのケースについて証明するのは、それなりに手順を踏まなくてはなりません。証明については、当サイトの『初等整数論講座』を参照してください。

【例題】$2$ と $3$ の最小公倍数を見つけて、公倍数を $5$ つ並べてください。
 
【解答】$2$ の倍数と $3$ の倍数を並べてみます。
 \[\begin{align*}&2,\ 4,\ 6,\ 8,\ 10,\ \cdots\\[6pt]&3,\ 6,\ 9,\ 12,\ 15,\ \cdots\end{align*}\]
最小公倍数は $6$ なので、$6$ の倍数
 \[6,\ 12,\ 18,\ 24,\ 30\]
が $2$ と $3$ の公倍数です。　

大きな数の最小公倍数

少し数が大きくなると倍数を並べて最小公倍数（LCM）を見つけるのは、とても大変です。例として $126$ と $210$ の最小公倍数を考えてみましょう。下図のように 2 つの数に共通な約数で割っていきます。
 

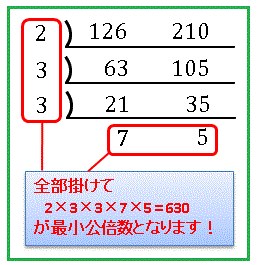
「これ以上は無理」というところまで割ります。すると
 \[\begin{align*}&126=2\cdot 3\cdot 3\cdot 5\tag{1}\\[6pt]&210=2\cdot 3\cdot 3\cdot 7\tag{2}\end{align*}\]
のように、積の形に分解されることがわかりますね。(1) に $7$、(2) に $5$ を掛けると、
 \[\begin{align*}
&126\cdot 7=2\cdot 3\cdot 3\cdot 5\cdot 7\\[6pt]
&210\cdot 5=2\cdot 3\cdot 3\cdot 5\cdot 7\end{align*}\]
となって同じ数に揃うことになります。つまりこれが最小公倍数となっているはずです。答えは
 \[2\cdot 3\cdot 3\cdot 5\cdot 7=630\]
となります。

【例題】$315$ と $495$ の最小公倍数を求めてください。
 
【解答】共通の約数で割っていくと …
 

 
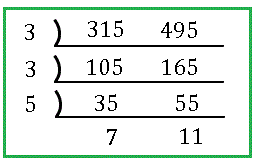
このようになります。現れた数を全て掛け合わせて
 \[3\cdot 3\cdot 5\cdot 7\cdot 11=3465\]
が最小公倍数となります。