右側極限と左側極限

【CL01】関数の右側極限と左側極限

関数 $f(x)$ を次のように定義します。
\[f(x)=\frac{1}{(x-1)^3}\](1) $\displaystyle \lim_{x\rightarrow 1+0}f(x)$ と \(\displaystyle \lim_{x\rightarrow 1-0}f(x)\) を求めてください。
(2) \(\displaystyle \lim_{x\rightarrow +\infty}f(x)\) と \(\displaystyle \lim_{x\rightarrow -\infty}f(x)\) を求めてください。
(3) \(f(x)\) のグラフの概形を描いてください。

【ヒント】関数の極限値を求める基本的な問題です。(1) の $x\rightarrow 1 + 0$ は 1 より大きい値をとりながら $1$ に近づく極限（右側極限）、$x\rightarrow 1 – 0$ は 1 より小さい値をとりながら $1$ に近づく極限（左側極限）です。
　
【解答】(1) 分母は $3$ 乗の形になっているので、その符号は右側極限では正に、左側極限では負になることに注意します。

\[\lim_{x\rightarrow 1+0}f(x)=+\infty,\quad \lim_{x\rightarrow 1-0}f(x)=-\infty\]
　右側極限は分母が $1$ よりほんの少し大きな値、左側極限は分母が $1$ よりほんの少し小さな値を代入するという感覚です。もう少し丁寧にするならば、たとえば左側極限は \(x=1-a\) とおいて、
 \[\lim_{a\rightarrow 0}f(x)=\lim_{a\rightarrow 0}\frac{1}{(1-a-1)^3}=\lim_{a\rightarrow 0}\frac{1}{(-a)^3}=-\infty\]
のように書きます。

(2) \(x\) が正負の無限大で 0 に近づくことは明らかです。
\[\lim_{x\rightarrow +\infty}f(x)=0,\quad \lim_{x\rightarrow -\infty}f(x)=0\]
となります。

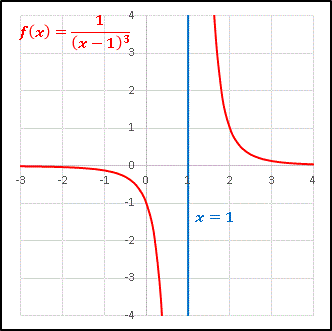
(3) (1) と (2) の結果をもとにグラフを描くと次のようになります。