今年 (2016 年) の夏、こばとちゃんはたくさんのお友達と一緒に足和田山(富士の山梨県側の麓にある山塊のひとつ)に登りました。色々なことがありましたけど、山頂から景色を眺めたり、お弁当やおやつを食べたり、とても愉快に過ごしました。そんな楽しい夏の思い出から問題を1つ。
【算数問題22】こばとちゃんは往復で何km歩いた?
こばとちゃんは羽根があるので登りも下りも飛行速度は変わりませんけど、全員が歩くのが一番遅い小春ちゃんに歩調を合わせなくてはいけません。皆で揃って時速 1.5 km の速さで山頂まで登り、そこでお弁当を食べたりして 2 時間ほど休憩して、それから時速 3 km の速さで下山しました。合計で 5 時間 30 分かかりました。こばとちゃん御一行は往復で何 km 歩きましたか。
【ヒント】線分を書いて比の関係ですぱっと解きたいところ。ちなみに足和田山に登るときの実際の歩行距離をそのまま使っています。
5 時間 30 分 - 2 時間 = 3 時間 30 分
さらに、「○○時間△△分」といったような記述は非常に計算しづらいので、分単位に直しておきましょう。
3 時間 30 分 = 3 × 60 + 30 = 210 分
ここで比の考え方に持ち込みます。まず 登りと下りの速さの比 は
1.5:3 = 3:6 = 1:2
となっていますね。
歩いた距離 = 速さ × 歩いた時間
という公式を眺めて、歩いた時間と速さは反比例の関係にある ことを思い出しましょう。つまり 210 分という時間を、下図のように登りと下りの速さで逆比例分配します。
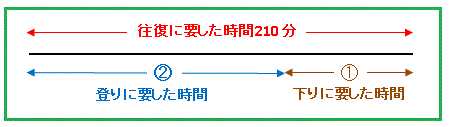
分けた線分の左側が登りにかかった時間、右側が下りにかかった時間です。具体的に計算すると、
登りにかかった時間 = 210 × 2/3 = 140 分 下りにかかった時間 = 210 × 1/3 = 70 分
となります。感覚的にも登りのほうが時間がかかると分かるので、とりあえず比で分けてしまえば、常識的にどちらにどのくらいの時間がかかったのかはすぐにわかります。あとは速さと時間をかけて答えを計算しますが、そこそこ切りのよい答えになりそうだと見通しが立てば、速さの単位は時間を分に直しておくだけで十分です(このへんはある程度直感で)。
登りで歩いた距離 = [1.5 km / 60 分] × 140 分 = 3.5 km
当たり前ですが、往復しているだけなので下りで歩いた距離も同じですから、上の値を 2 倍すれば答えが得られます。でも、念のために検算も兼ねて確認しておきましょう。
下りで歩いた距離 = [3 km / 60 分] × 70 分 = 3.5 km
ちゃんと合っていますね。答えは
2 × 3.5 = 7 km
となります。

エクセルや数学に関するコメントをお寄せください