二項展開と二項係数
二項和のべき乗 $(a+b)^n$ ($n$ は自然数) を展開することを二項展開(binomial expansion)といい、各項の係数を二項係数 (binomial coefficient)とよびます。具体的に展開式を並べてみましょう。
\[\begin{align*}(a+b)^1&=a+b\\[6pt](a+b)^2&=a^2+2ab+b^2\\[6pt](a+b)^3&=a^3+3a^2b+3ab^2+b^3\\[6pt]\cdots&\cdots\cdots\cdots\cdots\end{align*}\]
$a^{n-r}b^r$ の係数は規則的に現れます。この係数だけ抜き出してピラミッド状に並べたものをパスカルの三角形(Pascal’s triangle)とよびます。
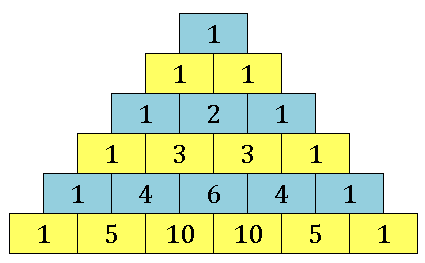
両端は全て 1 であり、内側は上段の 2 数の和が下段の数になっています。この規則さえ覚えておけば、二項展開における各項の係数を簡単に知ることができます。
二項定理
二項展開における係数を知る他の方法も見ておきましょう。展開するだけならパスカルの三角形のほうが断然早いのですが、ある種の証明問題には具体的な表式が必要になることがあります。たとえば $n=4$ として
\[(a+b)^4=(a+b)(a+b)(a+b)(a+b)\]
を展開するときに $a^2b^2$ はいくつ現れるのかを考えてみます。

図にあるように、4 つの括弧にあるうちの 2 つから $b$ をとるたびに、$a^2b^2$ という項が作られることになります。4 つの括弧から 2 つを選ぶ方法は
\[{}_4\mathrm{C}_2=6\]
なので、この展開式における $a^2b^2$ の係数は 6 であることがわかります。他の項についても同様に考えると、それぞれの項の係数は以下のようになります。
\[\begin{align*}a^4\qquad &{}_4\mathrm{C}_0=1\\[6pt]a^3b\qquad &{}_4\mathrm{C}_1=4\\[6pt]a^2b^2\qquad &{}_4\mathrm{C}_2=6\\[6pt]ab^3\qquad &{}_4\mathrm{C}_3=4\\[6pt]b^4\qquad &{}_4\mathrm{C}_4=1\end{align*}\]
よって $(a+b)^4$ は次のように展開されることになります。
\[(a+b)^4={}_4\mathrm{C}_0a^4+{}_4\mathrm{C}_1a^3b+{}_4\mathrm{C}_2a^2b^2+{}_4\mathrm{C}_3ab^3+{}_4\mathrm{C}_4b^4\]
一般の $n$ についても同様にして次の 二項定理 (binomial theorem) が得られます。
\[(a+b)^n=\sum_{k=0}^n{}_n\mathrm{C}_k\:a^{n-k}\:b^{\:k}\tag{A}\]
$\displaystyle{}_n\mathrm{C}_k=\binom{n}{k}$ と書くなら
\[(a+b)^n=\sum_{k=0}^n\binom{n}{k}a^{\:n-k}\:b^{\:k}\tag{B}\]
となります。二項定理に$a=1,\:b=x$ を代入すると
\[(1+x)^n=\sum_{k=0}^n{}_n\mathrm{C}_k\:x^{\:k}\]
となります。これは色々なところで使われる展開公式です。さらに $x=1$ とすれば
\[2^n=\sum_{k=0}^n{}_n\mathrm{C}_k\]
というように、$2^n$ を Combination の和で表すこともできます。
多項定理
$(a+b+c)^n$ の展開を考えてみます。
\[(a+b+c)^n=(a+b+c)(a+b+c)\cdots(a+b+c)\]
の展開式において $a^pb^qc^r$ という項は $p$ 個の括弧から $a$ をとり、$n-p$ 個の括弧から $c$ をとる組合せの数だけ作られます。よってその係数は
\[{}_n\mathrm{C}_p{}\:_{n-p}\mathrm{C}_q=\frac{n!}{(n-p)!}\frac{(n-p)!}{q!(n-p-q)!}\]
ここで $p+q+r=n$ なので
\[{}_n\mathrm{C}_p{}_{n-p}\:\mathrm{C}_q=\frac{n!}{p!q!r!}\]
となります。一般的な場合も同様にして
\[(a_1+a_2+\cdots+a_k)^n=\sum\frac{n!}{p_1!p_2!+\cdots p_k!}a_1^{p_1}a_2^{p_2}\cdots a_k^{p_k}\]
ただし $\sum$ は $p_1+p_2+\cdots+p_k=n$ を満たす全ての $p_1,\:p_2,\:\cdots,\:p_k$ についての和を表します。たとえば $(x+y+z)^6$ を展開したときの $x^3y^2z$ の係数は
\[\frac{6!}{3!2!1!}=60\]
というように計算できます。

エクセルや数学に関するコメントをお寄せください