ロルの定理と平均値の定理

この記事では、最初にロルの定理を証明し、そこから平均値の定理、コーシーの平均値の定理といった、より汎用性の高い定理を示していきます。

ロルの定理

ロルの定理は、曲線が滑らかで切れ目なくつながっていて、しかも異なる 2 点で同じ値をとるならば、その 2 点の間に $x$ 軸と平行な接線を引くことができると主張しています。

【ロルの定理の証明】ロルの定理を証明します。まず、下の図でイメージを掴んでください。
 

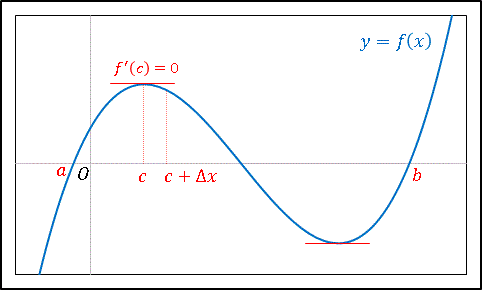
$f(x)=0$ のときは $f'(x)=0$ となって定理は成り立ちます。次に $f(x) \gt 0$ となる値がある場合を考えます。$f(x)$ は区間内で連続なので、ある点 $c$ で最大値をとることができるはずです。このとき
 \[f'(c)\gt 0,\quad f(a)=f(b)=0\]
なので $c$ は $a,\:b$ のどちらでもなく、
 \[a\lt c\lt b\]
という関係にあります。$f(c)$ は最大値なので、小さな値 $|\Delta x|$ に対して
 \[f(c+\Delta x)\leq f(c)\]
が成り立ちます。よって $\Delta x \gt 0$ のとき
 \[\frac{\Delta y}{\Delta x}=\frac{f(c+\Delta x)-f(c)}{\Delta x}\leq 0\]
となります。すなわち
 \[f'(c)=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}\leq 0\]
です。同様に $\Delta x \lt 0$ のとき $f'(c) \geq 0$ となるので、
 \[0\leq f'(c)\leq 0\]
すなわち $f'(c)=0$ が成り立ちます。$f(x) \lt 0$ となる値がある場合も同様の議論によって $f'(c)=0$ となるので、ロルの定理が成り立つことが証明されました。

平均値の定理

ロルの定理をより一般化した平均値の定理を解説します。

平均値の定理は曲線上の 2 点 $(a,\:f(a)),\:(b,\:f(b))$ を結ぶ線分と平行な接線がひけるような点 $(c,\:f(c))$ が区間内に存在することを主張しています。
 

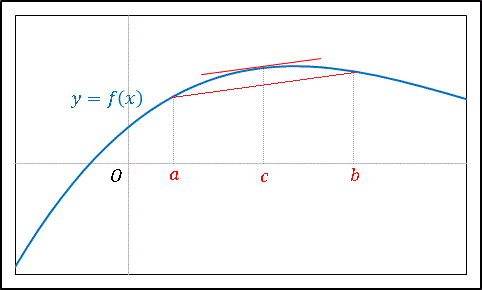
【平均値の定理の証明】数学者コーシー (Augustian Louis Cauchy) による巧みな証明法を紹介しましょう。
 \[m=\frac{f(b)-f(a)}{b-a}\]
とおきます。そして次のような関数
 \[F(x)=f(x)-f(a)-m(x-a)\]
をつくってみると $F(a)=0$ であり、また
 \[F(b)=f(b)-f(a)-m(b-a)=0\]
となります（こうなるように $F(x)$ を定義したのです）。つまり
 \[F(a)=F(b)=0\]
を満たし、$F'(x)=f'(x)-m$（微分可能）なので、ロルの定理より
 
\[F'(c)=0\quad (a\lt c\lt b)\]
となるような実数 $c$ が少なくとも 1 つは存在します。このとき $f'(c)=m$ ですから、
 \[\frac{f(b)-f(a)}{b-a}=f'(c)\]
が成り立ちます。平均値の定理を端点 $a$ と $b$ の差で表すこともできます。つまり
 \[b=a+h\]
とおくと $a$ と $b$ の間にある点 $c$ は
 \[c=a+\theta h \quad (0 \lt \theta \lt 1)\]
と表すことができるので、平均値の定理を以下のように書くことができます。

大学入試等で平均値の定理が題材になることは少ないですが、この定理は別名存在定理とよばれ、数学を発展させるために大きな貢献をしてきました。「なにかの存在を保証する」というのは、数学ではものすごい威力を発揮するのです（積分で表された平均値の定理はこちらを参照してください）。

コーシーの平均値の定理

平均値の定理をさらに一般化したのがコーシーの平均値の定理です。

$g(x)=x$ とすれば平均値の定理が得られます。
 
【コーシーの平均値の定理の証明】平均値の定理より
 \[g(b)-g(a)=(b-a)g'(d)\quad (a\lt d\lt b)\]
となる点 $d$ が存在します。$g'(d) \neq 0$ なので $g(b)-g(a) \neq 0$ です。
 \[\lambda =-\frac{f(b)-f(a)}{g(b)-g(a)}\]
という定数を定義して
 \[F(x)=f(x)+\lambda g(x)\]
という関数をつくります。$F(a)=F(b)$ なのでロルの定理が使えて
 \[F'(c)=f'(c)+\lambda g'(c)=0\]
を満たす点 $c$ が存在します。よって $\lambda$ は $c$ を用いて
 \[\lambda=-\frac{f'(c)}{g'(c)}\]
と表せるので
 \[\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)}\]
が成り立ちます。