モンティ・ホール問題（お得な箱の選び方）

[PS28] モンティ・ホール問題

南池袋の小さな AI が経営する出版会社『あとりえこばと』。
ある日の午後、社長のこばとちゃんは、アルバイトの沙希ちゃんにこんなゲームを持ちかけました。
「ここに A, B, C と書かれた３つの箱が並んでいますね。この中の１つに美味しいチョコレートケーキが入っています。どの箱に入っているかを当てたら、ケーキを食べていいですよ」


沙希ちゃんが「じゃあ、これ」と 1 つの箱を指差すと、こばとちゃんは
「本当にそれでいいんですか？　残りの箱の空のほうを開けてあげましょ～」
と言って、沙希ちゃんが選ばなかった２つの箱のうち、空の箱を選んで開けて見せます。それから、こんなことを言いました。
「沙希ちゃん、ここで選び直してもいいですよ」
こばとちゃんにそう言われて、沙希ちゃんは考え込みます。
「２つの箱のどちらかにケーキが入っているんだから、どちらにしたって確率は半々で同じはずだよね…」
本当にそうでしょうか？
最初に指差した箱と、もう１つの箱、沙希ちゃんはどちらを選ぶべきなのか考えてください。

【ヒント】有名な モンティ・ホール問題 です。当時の名だたる数学者たちでさえ間違えてしまった難問中の難問（？）なのですが、見方を間違えなければ、これほど単純な問題もありません。１分で答えられます。頭を柔らかくして考えてみてください。
　
【解答】この問題は基本に忠実に図を描くだけで簡単に解くことができます。沙希ちゃんが最初の選択を変えない場合、ケーキを当てる確率は $\displaystyle\frac{1}{3}$ です。沙希ちゃんが別の箱を選ぶ場合を考えてみましょう。

[A] 沙希ちゃんが最初に空箱を選ぶ確率は $\displaystyle\frac{2}{3}$ です。


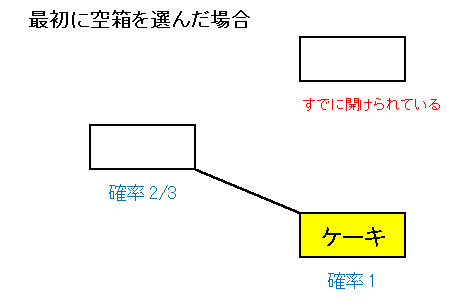
もちろん、このとき沙希ちゃんは自分の箱にケーキが入ってるかどうか知りません。しかし、こばとちゃんは残り２つの箱のうち空箱を選んで開けるので、沙希ちゃんが選択を変えると、自動的にケーキの入った箱を選択することになります。したがって、空箱を指差したあとにケーキを選ぶ確率は
\[\frac{2}{3} \times 1=\frac{2}{3}\]
となり、最初に空箱を指差す確率をそのまま受け継ぎます。

[B] 沙希ちゃんが最初にケーキの入った箱を選ぶ確率は 1/3 です。


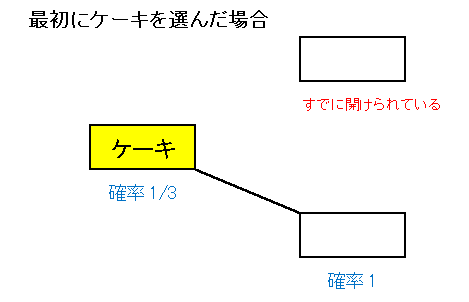
沙希ちゃんが選択を変えると、残念なことにケーキを失ってしまう結果になります。念のために計算すると、ケーキを失う確率は
\[\frac{1}{3}\times 1=\frac{1}{3}\]
となり、最初にケーキの箱を指差した確率を受け継ぎます。

以上より、沙希ちゃんは箱を選び直すと、ケーキを当てる確率は $\displaystyle\frac{2}{3}$ となり、最初の選択を変えないでいるよりも 2 倍も高い確率で当てることができるのです。

元ネタは『マリリンにおまかせ』です

その昔、モンティ・ホール (Monty Hall) が司会を務めるアメリカのショー番組でこんな問題が出されました。
「あなたの目の前に３つの扉があります。１つの扉の向こうには新車があり、残り２つの扉の後ろにはヤギがいます。新車の扉を開けることができれば車はあなたのものです！」
回答者が扉の１つを選択すると、司会者はヤギのいるほうの扉を開けて見せてくれます。
「ここで扉を選び直してもいいですよ？　さあ、どうします？」
回答者が最初に選んだ扉と、司会者が開けなかったほうの扉、はたしてどちらを選ぶべきなのでしょうか？

番組の司会者の名前をとってモンティ・ホール問題とよばれていますが、この問題の元ネタは、とある雑誌の「マリリンにおまかせ」という連載記事に読者から寄せられた問題です。実は回答者のマリリン・ボス・サヴァントは「世界で最も知能指数の高い女性」としてギネスブックに載るほどの天才的な頭脳をもつ人物でした。当然この問題に対しても見事に正解します。ところが、その解答が直感に反するものだったので、多くの読者から「彼女は間違っている！」という非難の手紙が殺到したのです。その中には多くの数学者や科学者も含まれていました。残念なことに、そのような人たちでさえ感情的になってマリリンを攻撃したのです。ていうか、そのような人たちだったからと言うべきですかね…だって、普通の人はそんなことしないし …数学者とか科学者ってさ…これ以上はやめておきます。

➡【PS01】各位がすべて異なる3桁の奇数