1/x^2の積分, 1/xの積分

1/x^2の積分

積分公式
\[\int x^{m}dx=\frac{1}{m+1}x^{m+1}\tag{1}\]
を使えば、$1/x^2$ の不定積分は簡単です：
\[\int\frac{1}{x^2}dx=\int x^{-2}dx=-\frac{1}{x}+C\tag{2}\]
しかし、定積分を求めるときは積分範囲に注意が必要です。$x=0$ を含む範囲では、$y=1/x^2$ を普通のやり方では積分できません。たとえば、何も考えずに上の公式を使って
\[\int_{-1}^{1}\frac{1}{x^2}dx=\left[ -\frac{1}{x} \right] _{-1}^{1}\tag{3}\]
を計算すると、$-2$ という不条理な値を得ます。$y=1/x^2$ のグラフを描いてみれば、積分値が負になることはまずありえないし、実際にはこの積分は $+\infty$ となることが理に適っていると考えるでしょう：


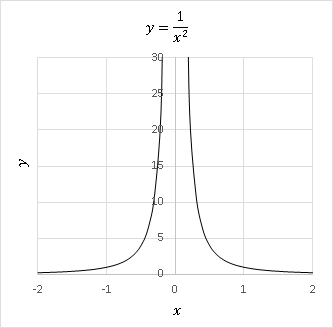
$y=1/x^2$ は原点で不連続なので、初等範囲（高校数学の範囲）では積分できないのです。しかし、原点にぎりぎり近い（つまり無限に小さな）区間 $[-\varepsilon,\ \varepsilon]$ を積分範囲から取り除くことで、直感に合った計算結果を得ることができます（このようなやり方をコーシーの主値積分とよびます）。

実際に試してみましょう。まず、$\varepsilon$ を適当に小さな値と考えて、被積分関数を区間 $[-1,\ -\varepsilon]$ と $[\varepsilon,\ 1]$ で別々に積分し、足し合わせます。
\[\int_{-1}^{1}\frac{1}{x^2}dx=\int_{-1}^{-\varepsilon}\frac{1}{x^2}dx+\int_{\varepsilon}^{1}\frac{1}{x^2}dx=\frac{1}{2\varepsilon}-2\tag{4}\]
$\varepsilon \rightarrow +0$ とすれば、
\[\int_{-1}^{1}\frac{1}{x^2}dx=+\infty\tag{5}\]
となります。

次の積分もよく登場するので覚えておくといいかもしれません。
\[\int \frac{dx}{x^{2}-a^{2}}=\frac{1}{2a}\: \log\left | \frac{x-a}{x+a} \right |+C\tag{6}\]
この公式は部分分数分解で簡単に証明できます：
\[\begin{align*}\int \frac{dx}{x^{2}-a^{2}}=&\int \frac{dx}{(x+a)(x-a)}\\[6pt]=&\frac{1}{2a}\int \left ( \frac{1}{x-a}-\frac{1}{x+a} \right )dx\\[6pt]=&\frac{1}{2a}\: \log\left | \frac{x-a}{x+a} \right |\end{align*}\tag{7}\]
(6) の被積分関数で $a = 1$ とおいた関数を $f(x)$ とおきます。
\[f(x)=\frac{1}{x^{2}-1}\tag{8}\]
$x \gt 0$ の範囲のグラフは次のようになります（偶関数なので $x \lt 0$ の領域は $x \gt 0$ の部分を折り返したグラフです）。



図中に示された任意の実数 $k (\gt 1)$ から $k + 1$ までの長さ 1 の線分と $f(x)$ で囲まれた面積 $S(k)$ の表式を求めてみます。(1) の公式を使うと
\[S(k)=\int_{k}^{k+1} \frac{dx}{x^{2}-1}=\log\left [ \frac{k(k+1)}{(k-1)(k+2)} \right ]\tag{9}\]
となりますね。図示すると下図のようになります。



やはり先程と同じような形の単調減少関数となります。
k を大きくしていくと、面積 $S(k)$ はどんどん小さくなります。
\[S(3/2)=0.381,\ S(2)=0.203,\ S(3)=0.091\]
$k=3$ を超えたあたりでは、もうほとんど面積はなくなってしまいます。

1/xの積分

$1/x^2$ と同様に、$1/x^3$ や $1/x^4$ の不定積分も公式 (1) を用いて求めることができますが、$1/x$ すなわち、$m=-1$ のときは、右辺の分母が $0$ となってしまうので、公式 (1) は使えません。

$\log x$ を微分すると $(\log x)’=1/x$ となります。
$\log x$ の定義域は $x \gt 0$ なので、この範囲に限定するなら、$1/x$ の不定積分は
\[\int\frac{1}{x}dx=\log x + C\tag{10}\]
ですが、全区間で微分を定義する場合は
\[\int\frac{1}{x}dx=\log |x| + C\tag{11}\]
となります。その理由は下図を見ると明らかです。


$f(x)=1/x$ の原始関数を $F(x)$ とすると、$f(x)$ は $F(x)$ の各点における接線の傾きを表しています。$f(x)=1/x$ は奇関数なので、$f(-x)=-f(x)$ です。つまり、$F(x)$ の接線が $y$ 軸に関して対称になるはずです。$F(x)=\log |x|$ は確かに、この条件を満たしています。

$1/x^2$ の積分のときと同様、$1/x$ も原点で定義されていないので、原点を跨ぐ積分を実行するときは、原点を取り除いて計算する必要があります。詳しくは 広義積分とコーシーの主値積分 に載っているので、気になる人は確かめてみてください。