円周上の２接点の間の距離

【AG22】２接点の間の距離を求めます

図のように原点を中心とした半径 $1$ の円があり、$y$ 軸上の点 $P(0,t)$ から、この円に接するように $2$ 本の直線を引きます $(t>1)$。２つの接点 Q, R を結んだ線分の長さを $L$ を $t$ で表し、$t$ が無限に大きくなったときの $L$ の値を求めてください。ただし、$t$ が無限に大きいときは $1/t^2=0$ として計算してください。
 

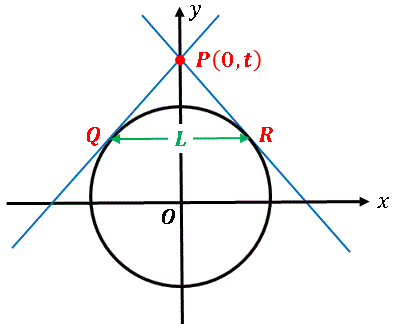
【ヒント】何となく直感で作ってみた問題です。ほとんどが数学Ⅰの内容です。最後のところで数学Ⅲで習う極限の概念を少し使いますが、数学Ⅲを未履修の人も、あまり難しく考えずに問題文で説明されているように計算してください。
　
【解答】直線の方程式を
 $$\begin{array}{}\text{(1)}& y=ax+t\end{array}$$
とおきます。半径 $1$ の円の方程式は
 $$\begin{array}{}\text{(2)}& x^2+y^2=1\end{array}$$
ですから、(1) を代入すると
 $$\begin{array}{rl}& x^2+(ax+t{)}^2=1\\ & \iff (a^2+1)x^2+2atx+t^2-1=0\end{array}$$
円と直線は接するのは、この方程式が重解をもつとき、すなわち判別式 $D/4=0$ となるときです。
 $$D/4=a^2{t}^2-(a^2+1)(t^2-1)=0$$
式を整理すると
 $$a^2-t^2+1=0$$
したがって、$a$ は $t$ によって
 $$a=\pm \sqrt{t^2-1}$$
と表せます（$\pm$ は２本の直線に対応しています）。また重解 $x$ は
 $$x=\frac{-at\pm \sqrt{D/4}}{a^2+1}$$
であり、$D/4=0$ なので、
 $$x=\frac{-at}{a^2+1}$$
となります。ここに $a$ を代入すると
 $$x=\frac{\pm t\sqrt{t^2-1}}{t^2}=\frac{\pm \sqrt{t^2-1}}{t}$$
のように $x$ を $t$ で表すことができます。この解の大きいほうを $\alpha$、小さいほうを $\beta$ とすると、接点を結ぶ線分の長さ $L$ は
 
$$L=\alpha -\beta =2\frac{\sqrt{t^2-1}}{t}=2\sqrt{1-\frac{1}{t^2}}$$
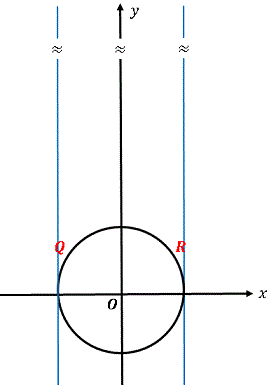
となります。$t$ を無限に大きくすると、$1/t^2=0$ ですから
 $$L=2\sqrt{1-0}=2$$
となります。つまり $y$ 軸上の無限遠点から引いた接線は $x=\pm 1$ で接し、接点を結ぶ線分の長さは円の直径に等しくなります。

【AG23】虚数解と実数解を２つずつもちます

四次方程式
$$x^4+x^3+px+q=0$$が２つの虚数解 $\alpha ,{\alpha }^2$ と２つの実数解をもつように定数 $p,q$ を定めてください。
 
【ヒント】「虚数解 $a+bi$ が解であるときに、その共役数 $a-bi$ もまた解である」という方程式の基本性質は既知とします。
　
【解答】虚数解の１つを $\alpha =a+bi$ とおくと、題意よりもう１つの解は ${\alpha }^2=a-bi$となります。したがって
 $$(a+bi{)}^2=a-bi$$
とおけます。展開して整理すると
 $$a^2-b^2-a+(2a+1)bi=0$$
となるので、実部と虚部をそれぞれ $0$ とおいて
 $$\begin{array}{rl}& a^2-b^2-a=0\\ & (2a+1)bi=0\end{array}$$
$\alpha$ は虚数解なので、$b\ne 0$ です。よって
 $$a=-\frac{1}{2},b=\pm \frac{\sqrt{3}}{2}$$
となって、$\alpha$ と ${\alpha }^2$ は
 $$-\frac{1\pm \sqrt{3}i}{2}$$
となります。ここで
 $$\alpha +{\alpha }^2=-1,\alpha \cdot {\alpha }^2=1$$
と計算できるので、解と係数の関係より $\alpha$ と ${\alpha }^2$ を２解とする方程式は
 $$x^2+x+1=0$$
となります。求める四次方程式は実数解をもつので、
 $$x^4+x^3+px+q=(x^2+x+1)(x^2-c)$$
と因数分解できるはずです。右辺を展開すると
 $$x^4+x^3+px+q=x^4+x^3+(1-c)x^2-cx-c$$
となるので、両辺の係数を比べて
 $$c=1,p=-1,q=-1$$
と決まります。よって求める四次方程式は
 $$x^4+x^3-x-1=0$$
となります。

【AG24】三元三次連立方程式

次の方程式を解いて $x,y,z$ を求めてください。
$$\begin{array}{rl}x+y+z=& 3\\ x^2+y^2+z^2=& 35\\ x^3+y^3+z^3=& 99\end{array}$$ただし $x<y<z$ とします。
 
【ヒント】解と係数の関係 を使うと楽です。
　
【解答】いずれにしろ最高次数が $3$ なので、最終的には三次方程式を解くことになるはずです。そこで三次方程式の解と係数の関係を用いるために
 $$x+y+z,xy+yz+zx,xyz$$
の値が必要となります。$x+y+z$ はすでに与えられています。式をじっと見つめると、１つめの式の平方から $x^2+y^2+z^2$ (問題文の条件より定数になります) と $xy+yz+zx$ の形をひっぱり出せることは予測できるので、まずはここから手をつけてみましょう。
 $$(x+y+z{)}^2=x^2+y^2+z^2+2(xy+yz+zx)$$
と展開できるので、$x^2+y^2+z^2=35$ を代入して
 $$xy+yz+zx=-13$$
を得ることができます。残るは $xyz$ ですが、これを問題文の式から出すことは面倒なので、それはもう未知数のままにして、この段階で思いきって $xyz=k$ とおいて、解と係数の関係から三次方程式をつくってしまいましょう。
 $$t^3-3t^2-13t-k=0$$
となりますね（忘れた人はここで公式を確認してくださいね … なんて偉そうなことを言いながら、私も度忘れしてたけど）。$x,y,z$ がこの方程式をみたすので、
 $$\begin{array}{rl}{x}^3-3x^2-13x-k=& 0\\ y^3-3y^2-13y-k=& 0\\ z^3-3z^2-13z-k=& 0\end{array}$$
が成立します（当たり前です）。何でわざわざこんな式を３つも作ったのかというと、この３式を辺々足し合わせると $x,y,z$ が全て消えてしまうからです。すごいですね。これはちょっとしたテクニックなので覚えておいて損はありません。それでは足してみましょう。
 $$(x^3+y^3+z^3)-3(x^2+y^2+z^2)-13(x+y+z)-3k=0$$
これに与えられた方程式
 $$\begin{array}{rl}x+y+z=& 3\\ x^2+y^2+z^2=& 35\\ x^3+y^3+z^3=& 99\end{array}$$
を代入すると $x,y,z$ は消えて $k=-15$ を得ます。したがって $x,y,z$ は三次方程式
 $$t^3-3t^2-13t+15=0$$
の解であることが判明しました。$t=1$ が解であることは明らかなので、$t-1$ で割り算して
 $$\begin{array}{rl}& (t-1)(t^2-2t-15)=0\\ & (t-1)(t-5)(t+3)=0\end{array}$$
したがって、$t=1,5,-3$ が解となりますが、$x<y<z$ という条件があるので、
 $$(x,y,z)=(-3,1,5)$$
というように $x,y,z$ は１つに決まります。