3または5で割り切れる100以下の自然数の和

【SQ05】3または5で割り切れる数の総和

$100$ 以下の自然数で、$3$ または $5$ で割り切れる数の和を求めてください。

【ヒント】足し過ぎ（？）に注意です。

　
【解答】$100$ 以下の $3$ の倍数を並べてみます。
\[3,\:6,\:9,\:\cdots,\:96,\:99\]
これは初項 $3$, 末項 $99$ の等差数列です。和を求めるには項数 $n$ が必要です。
$n$ は $100$ を $3$ で割って、余りを切り捨てて $33$ です。ガウスの記号 $[x]$ を使うと
\[n=\left[\frac{100}{3}\right]=33\]
というように求めることができます。$[x]$ は $x$ を超えない整数という意味です。初項 $a_1$, 末項 $a_l$, 項数 $n$ の等差数列の和の公式は
\[S=\frac{n(a_1+a_l)}{2}\]
で与えられるので、$100$ 以下の $3$ の倍数の和は
\[S_{(3)}=\frac{33(3+99)}{2}=1683\]
となります。次は $5$ の倍数を並べます。
\[5,\:10,\:15,\:\cdots,\:85,\:100\]
初項 $5$, 末項 $100$ の等差数列です。項数は
\[n=\left[\frac{100}{5}\right]=20\]
なので、$100$ 以下の $5$ の倍数の和は
\[S_{(5)}=\frac{20(5+100)}{2}=1050\]
となります。ここで $S_{(3)}$ と $S_{(5)}$ を足し合わせると、ちょっと足し過ぎになります。

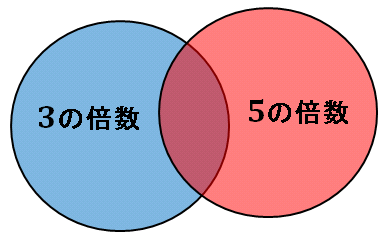
$S_{(3)}$ と $S_{(5)}$ をそのまま足してしまうと、上の図のように、「$3$ の倍数かつ $5$ の倍数」の部分を余計に加えてしまっていることになります。したがって、この部分、すなわち「$3$ と $5$ の最小公倍数 $15$ で割り切れる数」を差し引かなくてはなりません。$15$ の倍数を並べてみると
\[15,\:30,\:45,\:\cdots,\:75,\:90\]
これは初項 $15$, 末項 $90$ の等差数列です。項数は
\[n=\left[\frac{100}{15}\right]=6\]
なので、$100$ 以下の $15$ の倍数の和は
\[S_{(15)}=\frac{6(15+90)}{2}=315\]
となります。したがって、求める数は
\[S_{(3)}+S_{(5)}-S_{(15)}=1683+1050-315=2418\]
となります。

【SQ06】10と80の間にk個の数を入れます

$10$ と $80$ の間に $k$ 個の数を入れて等差数列をつくると総和が $495$ になりました。$k$ の値と公差を求めてください。

【ヒント】等差数列の和は初項と末項、項数によって計算します。

　
【解答】$10$ と $80$ の間に入れる $k$ 個の数を $a_n\:(n=1,\:2,\:\cdots,\:k)$ とすると、
\[10,\:a_1,\:a_2,\:\cdots,\:a_k,\:80\]
すなわち、項数 $k+2$ の等差数列になります。
初項 $a_1$、末項 $a_l$、項数 $n$ の等差数列の総和は
\[S=\frac{n(a_1+a_l)}{2}\]
で与えられるので、
\[495=\frac{(k+2)(10+80)}{2}\]
これを解いて $k=9$ が得られます。
$80$ は初項から数えて $11$ 番目の項なので、公差を $d$ とすると
\[80=10+(11-1)d\]
したがって、求める公差は $d=7$ です。

【SQ07】各項の逆数が等差数列

数列 $\displaystyle\left\{\frac{1}{a_n}\right\}$ は等差数列をなし、$a_4=6,\:a_6=4$ です。一般項 $a_n$ を求めて $a_{10}$ を計算してください。（福岡大一部改）

【ヒント】公差を求めましょう。

　
【解答】数列 $\displaystyle\left\{\frac{1}{a_n}\right\}$ の公差を $d$ とすると
\[f(x)=\begin{cases}\displaystyle\frac{1}{a_6}-\frac{1}{a_5} &=d\\[6pt]\displaystyle\frac{1}{a_5}-\frac{1}{a_4} &=d\end{cases}\]
が成り立ちます。すなわち、
\[f(x)=\begin{cases}\displaystyle\frac{1}{4}-\frac{1}{a_5} &=d\\[6pt]\displaystyle\frac{1}{a_5}-\frac{1}{6} &=d\end{cases}\]
これを解いて $d=\displaystyle\frac{1}{24}$ となります。
$\displaystyle\frac{1}{a_4}$ から公差の $3$ 倍を引けば初項が得られます。
\[\frac{1}{a_1}=\frac{1}{a_4}-3d=\frac{1}{6}-\frac{1}{8}=\frac{1}{24}\]
したがって、等差数列 $\displaystyle\left\{\frac{1}{a_n}\right\}$ の一般項は
\[\frac{1}{a_n}=\frac{1}{24}+\frac{n-1}{24}=\frac{n}{24}\]
となります。よって $a_n$ は
\[a_n=\frac{24}{n}\]
と表せます。$a_{10}$ を計算すると
\[a_{10}=\frac{12}{5}\]
となります。

【SQ08】三次方程式の３つの解が等差

方程式 $x^3-9x^2+2x+k=0$ の $3$ 解が等差であるとき、$k$ の値と解を求めてください。

【ヒント】$3$ 個の解を等差であるような形で表しましょう。しかし、それを直接方程式に入れると計算が大変です。

　
【解答】こういう問題では解と係数の関係を使うのがセオリーです。公差を $d$ として、求める $3$ 解を
\[a-d,\:a,\:a+d\:(d\gt 0)\]
とおくと（対称なので $d\lt 0$ としても同じです）、解と係数の関係より、
\[\begin{align*}&(a-d)+a+(a+d)=9\\[6pt]&(a-d)a+a(a+d)+(a-d)(a+d)=2\\[6pt]&(a-d)a(a+d)=-k\end{align*}\]
が成り立ちます。これを解くと $a=3,\:d=5,\:k=48$ が得られます。求める $3$ 個の解は
\[(a-d,\:a,\:a+d)=(-2,\:3,\:8)\]
となります。

【SQ09】２種類の数列の共通項を並べます

初項 $2$、公差 $3$ の等差数列を $\{a_n\}$、初項 $1$、公差 $5$ の等差数列を $\{b_n\}$ とします。$\{a_n\}$ と $\{b_n\}$ に共通する項を並べた数列 $\{c_n\}$ の一般項を求めてください。

【ヒント】整数と数列の融合問題です。$\{a_n\}$ と $\{b_n\}$ を具体的に書き並べてみると、なんとなく答えが予想できるかもしれません。

【考え方】問題を解く前に数列 $\{a_n\}$ と $\{b_n\}$ を並べてみます。
\[\begin{align*}&a_n=2,\:5,\:8,\:11,\:14,\:17,\:20,\:23,\:26,\:29,\:32,\:\cdots\\[6pt]&b_n=1,\:6,\:11,\:16,\:21,\:26,\:31,\:36,\:41,\:46,\:51,\:\cdots\end{align*}\]
$11$ と $26$ が一致しています。公差 $3$ と $5$ の最小公倍数は $15$ なので、$c_n$ はおそらく $15n-4$ という形になっていると予測できます。もちろん正式な解答では任意の $n$ についてそれが成り立っていることを証明しなくてはなりません。

　
【解答】条件式の両辺が等しくなるためには左辺が約数をもつ必要があります

数列 $\{a_m\}$ と $\{b_m\}$ の一般項はそれぞれ
\[\begin{align*}&a_m=2+3(m-1)=3m-1\\[6pt]&b_n=1+5(n-1)=5n-4\end{align*}\]
$a_m=b_n$ とおくと、
\[3m-1=5n-4\]
式を整理すると
\[3(m+1)=5n\]
となります。ここで左辺と右辺が等しくなるためには、左辺は $5$ を約数にもっていなければなりません。しかし、$3$ と $5$ の最大公約数は $1$ ですから（すなわち $3$ と $5$ は互いに素なので）、お互いを約数にもちません。よって、$m+1$ の約数の中に $5$ があるはずです。すなわち
\[m+1=5k\]
とおくことができます。したがって $a_{5k-1}$ が 数列 $c_m$ の各項と一致します。
\[a_{5k-1}=3(5k-1)-1=15k-4\quad (k=1,\:2,\:\cdots)\]
よって、求める数列 $\{c_n\}$ の一般項は
\[c_n=15n-4\quad (n=1,\:2,\:\cdots)\]
となります。

【SQ10】等差数列であるための必要十分条件

数列 $\{a_n\}$ の初項 $a_1$ から第 $n$ 項までの和を $S_n$ とします。$S_n=pn^2+qn+r$ ($r,\:p,\:q$ は定数) のとき、$\{a_n\}$ が等差数列であるための必要十分条件を求めてください。（相模工大）

【ヒント】
やや難度の高い問題。$S_n$ と $a_n$ の関係を使います。この問題の結論は覚えておきたいところです。

【考え方】等差数列の第 $n$ 項は $S_n$ から $S_{n-1}$ を差し引いた形で表せます。
\[a_n=S_n-S_{n-1}\quad (n\geq 2)\]
ただし、$n=1$ のときは $S_1=a_1$ です。

　
【解答】$n\geq 2$ のとき、
\[\begin{align*}a_n&\,=S_n-S_{n-1}\\[6pt]&\,=pn^2+qn+r-\{p(n-1)^2+q(n-1)+r\}\\[6pt]&\,=p+q+2p(n-1)\end{align*}\]
公差 $d$ の等差数列の一般項は $a_n=a_1+(n-1)d$ なので、
\[a_2,\:a_3,\:a_4,\:\cdots\]
は公差 $2p$ の等差数列であることがわかります。したがって、
\[a_2-a_1=2p\tag{1}\]
という条件さえ満たせば、$a_1$ も含めて $\{a_n\}$ は等差数列になります。$S_n$ を使って左辺を計算すると
\[\begin{align*}a_2-a_1&\,=(S_2-S_1)-S_1=S_2-2S_1\\[6pt]&\,=4p+2q+r-2(p+q+r)\\[6pt]&\,=2p-r\end{align*}\]
したがって、条件式 (1) は
\[2p-r=2p\]
となるので、$\{a_n\}$ が等差数列であるための必要十分条件は $r=0$ です。