ライプニッツの公式

ライプニッツの公式とよばれる定理は二種類あって、ひとつは関数の積 $f(x)g(x)$ の $n$ 階微分の一般表式（ライプニッツ則）、もうひとつは円周率の値を求める級（グレゴリー・ライプニッツ級数）です。この記事では両方を説明します。

f(x)g(x)のn階微分を求めるライプニッツの公式

$x$ の関数 $f(x)$ と $g(x)$ の積を微分すると、
\[(fg)’=f’g+fg’\]
となります。以後、記号を統一するために $f(x)$ の $n$ 次導関数を $f^{(n)}$ で表すことにすると、積の微分公式は
\[(fg)^{(1)}=f^{(1)}g^{(0)}+f^{(0)}g^{(1)}\]
と表せます。この式をもう１度微分すると
\[\begin{align*}(fg)^{(2)}&=f^{(2)}g^{(0)}+f^{(1)}g^{(1)}+f^{(1)}g^{(1)}+f^{(0)}g^{(2)}\\[6pt]&=f^{(2)}g^{(0)}+2f^{(1)}g^{(1)}+f^{(0)}g^{(2)}\end{align*}\]
となります。さらにもう１度微分すると
\[\begin{align*}(fg)^{(3)}&=f^{(3)}g^{(0)}+f^{(2)}g^{(1)}+2f^{(2)}g^{(1)}+2f^{(1)}g^{(2)}+f^{(1)}g^{(2)}+f^{(2)}g^{(3)}\\[6pt]&=f^{(3)}g^{(0)}+3f^{(2)}g^{(1)}+3f^{(1)}g^{(2)}+f^{(0)}g^{(3)}\\[6pt]\end{align*}\]
となります。この結果は $(a+b)^3$ の展開式
\[(a+b)^3=a^3+3a^2b+3ab^2+b^3\]
とよく似ています（各項の係数は同じで、冪乗を微分階数に置き換える形になっています）。したがって、$fg$ の $n$ 次導関数は二項展開の一般表式
\[\begin{align*}(a+b)^n=&\sum_{r=0}^n{}_n\mathrm{C}_r\ a^{n-r}\ b^{\ r}\\[6pt]=&\quad\,{}_n\mathrm{C}_0\ a^n\ b^0\\[6pt]&+{}_n\mathrm{C}_1\ a^{n-1}\ b^1\\[6pt]&+{}_n\mathrm{C}_2\ a^{n-2}\ b^2\\[6pt]&+\cdots\cdots\\[6pt]&+{}_n\mathrm{C}_{n-1}\ a^{1}\ b^{n-1}\\[6pt]&+{}_n\mathrm{C}_n\ a^0\ b^n\end{align*}\]
の形から、
\[\begin{align*}(fg)^{(n)}&=\sum_{r=0}^{n}{}_n\mathrm{C}_r\,f^{(r)}g^{(n-r)}\\[6pt]=&\quad \,{}_n\mathrm{C}_0\,f^{(n)}g^{(0)}\\[6pt]&+{}_n\mathrm{C}_1\,f^{(n-1)}g^{(1)}\\[6pt]&+{}_n\mathrm{C}_2\,f^{(n-2)}g^{(2)}\\[6pt]&+\ \cdots\cdots\\[6pt]&+{}_n\mathrm{C}_{n-1}\,f^{(1)}g^{(n-1)}\\[6pt]&+{}_n\mathrm{C}_n\,f^{(0)}g^{(n)}\end{align*}\]
となることが予想できます (ライプニッツの公式)。

【ライプニッツの公式の証明】
推測が正しいことを、数学的帰納法を使って証明してみます。$n=1$ のとき、
\[(fg)^{(1)}=f^{(1)}g^{(0)}+f^{(0)}g^{(1)}={}_1\mathrm{C}_0\ f^{(1)}g^{(0)}+{}_1\mathrm{C}_1\ f^{(0)}g^{(1)}\]
となって、確かに成立しています。$n=k$ のときに
\[\begin{align*}(fg)^{(k)}=&\sum_{r=0}^{k}{}_n\mathrm{C}_r\,f^{(r)}g^{(k-r)}\\[6pt]=&\quad \,{}_k\mathrm{C}_0\,f^{(k)}g^{(0)}\\[6pt]&+{}_k\mathrm{C}_1\,f^{(k-1)}g^{(1)}\\[6pt]&+{}_k\mathrm{C}_2\,f^{(k-2)}g^{(2)}\\[6pt]&+\ \cdots\cdots\\[6pt]&+{}_k\mathrm{C}_{k-1}\,f^{(1)}g^{(k-1)}\\[6pt]&+{}_k\mathrm{C}_k\,f^{(0)}g^{(k)}\end{align*}\]
が成り立つことを仮定します。この式を $x$ で微分します。
\[\begin{align*}(fg)^{(k+1)}=&\quad \,{}_k\mathrm{C}_0\,\{f^{(k+1)}g^{(0)}+f^{(k)}g^{(1)}\}\\[6pt]&+{}_k\mathrm{C}_1\,\{f^{(k)}g^{(1)}+f^{(k-1)}g^{(2)}\}\\[6pt]&+{}_k\mathrm{C}_2\,\{f^{(k-1)}g^{(2)}+f^{(k-2)}g^{(3)}\}\\[6pt]&+\ \cdots\cdots\\[6pt]&+{}_k\mathrm{C}_{k-1}\,\{f^{(2)}g^{(k-1)}+f^{(1)}g^{(k)}\}\\[6pt]&+{}_k\mathrm{C}_k\,\{f^{(1)}g^{(k)}+f^{(0)}g^{(k+1)}\}\end{align*}\]
ここで、公式 ${}_n\mathrm{C}_{r-1}+{}_n\mathrm{C}_r={}_{n+1}\mathrm{C}_r$ を使うと、
\[\begin{align*}(fg)^{(k+1)}=&\quad \,{}_k\mathrm{C}_0\,f^{(k+1)}g^{(0)}\\[6pt]&+({}_k\mathrm{C}_0+{}_k\mathrm{C}_1)f^{(k)}g^{(1)}\\[6pt]&+({}_k\mathrm{C}_1+{}_k\mathrm{C}_2)f^{(k-1)}g^{(2)}\\[6pt]&+\ \cdots\cdots\\[6pt]&+({}_{k}\mathrm{C}_{k-1}+{}_k\mathrm{C}_k)f^{(1)}g^{(k)}\\[6pt]&+{}_k\mathrm{C}_k\ f^{(0)}g^{(k+1)}\end{align*}\]
　${}_k\mathrm{C}_0={}_{k+1}\mathrm{C}_0={}_k\mathrm{C}_k={}_{k+1}\mathrm{C}_{k+1}=1$ なので、${}_k\mathrm{C}_0$ と ${}_{k+1}\mathrm{C}_0$ に、${}_k\mathrm{C}_k$ を ${}_{k+1}\mathrm{C}_{k+1}$ に置き換えることができて、
\[\begin{align*}(fg)^{(k+1)}=&\quad \,{}_{k+1}\mathrm{C}_0\,f^{(k+1)}g^{(0)}\\[6pt]&+({}_k\mathrm{C}_0+{}_k\mathrm{C}_1)f^{(k)}g^{(1)}\\[6pt]&+({}_k\mathrm{C}_1+{}_k\mathrm{C}_2)f^{(k-1)}g^{(2)}\\[6pt]&+\ \cdots\cdots\\[6pt]&+({}_{k}\mathrm{C}_{k-1}+{}_k\mathrm{C}_k)f^{(1)}g^{(k)}\\[6pt]&+{}_{k+1}\mathrm{C}_{k+1}f^{(0)}g^{(k+1)}\end{align*}\]
となり、$n=k+1$ のときも成立していることがわかります (証明終)。

ライプニッツの公式の一般表式における係数は ${}_n\mathrm{C}_r$ で表されていますが、実際の計算ではパスカルの三角形を使って係数を得る方が効率的です。$f^{(r)}g^{(n-r)}$ は $f$ と $g$ の微分階数が足して $n$ になるようにします。一例として、$fg$ の 三次導関数の求め方を載せておきます。

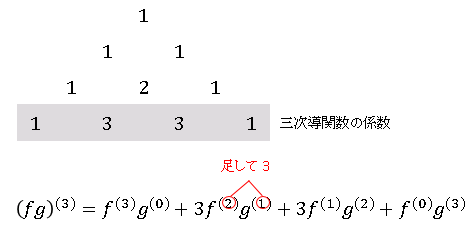
実際の計算でライプニッツの公式を適用する機会はそう多くないかもしれません。ほとんどの場合、順次微分して導関数を得た方が簡単で、四次以上の導関数が必要となるケースも稀だからです。それでも比較的単純な微分計算で、ライプニッツの公式を使うと見通しがよくなる場合もあります。一例として $y=x\cos x$ の微分を実行してみましょう。$f(x)=x,\ g(x)=\cos x$ と考えて、$fg$ の三次導関数
\[(fg)^{(3)}=f^{(3)}g^{(0)}+3f^{(2)}g^{(1)}+3f^{(1)}g^{(2)}+f^{(0)}g^{(3)}\]
において、$f^{(2)}$ と $f^{(3)}$ は $0$ なので、
\[(fg)^{(3)}=3f^{(1)}g^{(2)}+f^{(0)}g^{(3)}\]
を計算すればよいことになります。
\[f^{(0)}=x,\ f^{(1)}=1,\ g^{(2)}=-\cos x,\ g^{(3)}=\sin x\]
なので、
\[(fg)^{(3)}=-3\cos x+x\sin x\]
が得られます。このように $f(x)$ または $g(x)$ が $x$ のべき乗であれば、ある $n$ で $x^{(n)}$ が $0$ になるので、いくつもの項をごっそり落とすことができ、計算ミスを減らせます。

円周率の近似値を計算するライプニッツの公式

円周率 $\pi$ の $1/4$ は、以下の無限級数で表されることが知られています（グレゴリー・ライプニッツ級数）：
\[\frac{\pi}{4}=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}\]
ライプニッツ級数を書き下すと次のようになります。
\[\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11} \cdots\]
分母が奇数の交代級数だと理解しておくと覚えやすいです。
ただし、この級数は恐ろしく収束が遅いです。円周率の真値は 3.141592654 ですが … Excel を使って調べてみると、299 項とっても、3.138259 という値にしかならない … 。興味のある人は下のワークブックをダウンロードしてみてください。

≫ leibniz_pi.xslx をダウンロードする

このファイルの Calculation シートに計算結果が載っていますが、1000 項 (n=999) まで計算しても真値と 3 桁までしか一致しません。
「この公式、実は全く役に立たないのでは！？」
という暴論さえ頭に浮かびました。Excel で高精度の値が出るまで計算させると、動作が重たくなりそうなので、VBA で関数を作って計算させてみることにしました。

'[VBA]ライプニッツの公式で円周率の近似値を計算する関数

Function Leibniz_pi(n_end As Long)

　　Dim n As Long
　　Dim s As Double

　　'級数の初項
　　s = 1

　　'ライプニッツの公式で級数を計算
　　For n = 1 To n_end
　　　　s = s + (-1) ^ n / (2 * n + 1)
　　Next n

　　'円周率の近似値
　　Leibniz_pi = 4 * s

End Function

たとえば、セルに「=Leibniz_pi(1e6+1)」と入力すると ようやく 3.141591654 という値が得られます … 100 万ループなんてメモリの無駄遣いです。円周率の数値計算にライプニッツの公式はあまりおすすめできません。