【Excel】f(x)=x^n*exp(-x)のグラフ解析

この記事では、Excel で f(x)=x^n*exp(-x) のグラフをプロットして様々な視点で解析します。

nが偶数のときだけ極値をとります

微積分を学び始めた段階では
 \[f(x)=x\exp{(-x)}\tag{1}\]
のグラフを描けという問題は必ず出ます。積の微分公式を用いて
 \[f'(x)=(1-x)\exp{(-x)}\]
が得られますから
 \[f'(1)=0\]
となることがわかります。前後の符号を調べると
 \[f'(0)=1\gt 0,\quad f'(2)=-\exp(-2)\lt 0\]
となって $f(1)=1/e$ は 極大値 かつ最大値です。また、
 \[\begin{align*}\lim_{x\rightarrow+\infty}f(x)&=0\\[6pt]\lim_{x\rightarrow-\infty}f(x)&=-\infty\end{align*}\]
となるので、おおよその概形はイメージできると思います。
 
Excel のグラフで確認してみましょう。
 

イメージと合っていましたか？　この記事ではさらに一般化して、
 \[f(x)=x^n\exp{(-x)}\tag{2}\]
という関数を扱いますが、まず先に $n=2,\ 3$ のグラフを見てみましょう。
 

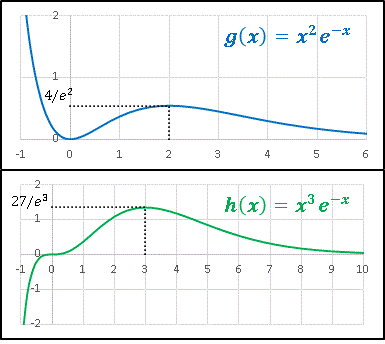
$n=2$ のときは極値は２つありますが、$n=3$ のときは１つだけです。それぞれの関数を別個に解析してもいいですが、ここは (2) を使ってより一般的な解析を試みます。微分して式を整理すると
 \[f'(x)=x^{n-1}(n-x)\exp{(-x)}\]
となります。$f’=0$ となるのは $x=0,\ n$ の 2 点ですね。$\delta$ という非常に小さな正数を示す記号を使って、この 2 点が極値であるかどうかを確認してみます。まず $x=0$ の前後の点を $x=+\delta,\ -\delta$ と表してみます。
 \[f'(+\delta)=\delta^{n-1}(n-\delta)\exp(-\delta)\gt 0\]
この関係は常に成立しますが、
 \[f'(-\delta)=(-\delta)^{n-1}(n+\delta)\exp(\delta)\]
については、$n$ が偶数のとき $f'(-\delta)\lt 0$, $n$ が奇数のとき $f'(-\delta)\gt 0$ となり、すなわち $n$ が偶数のときのみ $f'(x)$ の符号が変わって $f(x)$ は $x=0$ で極値をとることがわかります。先ほどの 3 枚のグラフで確認しておいてください。同じように $x=n$ の前後の点を $n+\delta,\ n-\delta$ と表すと
 \[\begin{align*}f'(n+\delta)=(n+\delta)^{n-1}(-\delta)\exp(-n-\delta)\lt 0\\[6pt]f'(n-\delta)=(n-\delta)^{n-1}\delta\exp(-n+\delta)\gt 0\end{align*}\]
となり $x=n$ の前後で $f'(x)$ の符号が変わって極値をとることがわかります。

グラフ全体を下に押し下げて平たくなる関数

ある１つの関数の性質を深く掘り下げていくと、他の色々な関数について知見を得られることがあるものです。$f(x)=\exp(x)/x^n$ について $n$ を変化させてグラフを描くと …
 

このようになります。$n$ の増加に応じて $x^n$ で割ることによる減衰効果が強くなり、グラフ全体を下に押し下げると同時に平たくなっていきますね。$f(1)=3$ ですから $n$ の値にかかわらず $(1,\ e)$ の点を通ることになります。また最小値も右下へずれていくことが見てとれます。微分して確認しておきましょう。
 \[\begin{align*}f(x)&=e^{x}x^{-n}\\f'(x)&=e^{x}(x^{n}-nx^{-n-1})=\left [\frac{x-n}{x^{n+1}} \right ]e^{x}\end{align*}\]
$f(x)’=0$ となる点は $x=n$ なので $n$ が $1$ ずつ増えると最小値を与える $x$ 座標も $1$ ずつ正方向へずれていきます。最小値は $f(n)=\exp(n)/n^n$ で与えられます。

最小値 $f(n)$ は
 \[g(x)=\frac{e^{x}}{x^{x}}\]
という曲線上の離散的な点として表せます。その様子を図示したのが下図です。
 

 
赤丸がとりうる最小値を表しています。$n$ の増加と共に最小値は $0$ に収束していく様子がわかりますね。また、$x^x$ が $\exp{(x)}$ よりも発散の速い関数だということもわかります。

それでは $y=x^x$ と $y=e^x$ を実際にグラフに並べて比較してみましょう。
 

ちょうど $x = e$ を境に両曲線の大小関係が逆転しているのがわかります。
$y=x^x$ は「底」も「指数」も同時に大きくなっていく関数なので、普通の指数関数に比べると値の増加は極めて大きいです。

xのn乗根を変数にもつ指数関数

指数関数に $x$ の $n$ 乗根を組込んだ $y=\exp \sqrt[n]{x}$ という関数を調べてみましょう。$n=2,\ 3,\ 4$ のグラフを描いてみます。
 

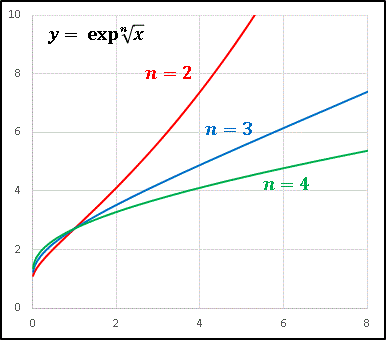
指数関数とはいっても、$n=3$ ではすでに直線 ($y=x$) と同程度の増加率しかありません。実際、$n=2$ から $n=3$ への変遷はグラフの性質を本質的に変えるもので、それは $y$ を微分して
 \[y’=\frac{1}{n}\,x^{1/n-1}\,\exp\sqrt[n]{x}\]
という導関数を調べるとより明らかになります。
 

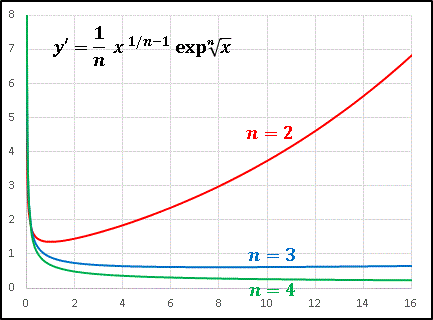
$n=2$ では $y’$ はある所から常に増加し続ける関数です。これは $\sqrt{x}$ よりも $\exp{\sqrt{x}}$ の効果のほうが大きいからです。しかし、$n=3$ では $x^{-2/3}$ と $\exp(x^{-1/3})$ が拮抗して $y’$ はほぼ一定値をとります。つまり、$y$ は直線のような関数となります。そして $n=4$ では $x^{-3/4}$ が $\exp(x^{-1/4})$ の寄与を少しだけ上回って $y’$ は減少します。このとき $y$ はその増加率を少しずつ減少させていきます。
　
このように、$x$ が大きくなるにしたがって増加率を緩める関数として対数関数が思い浮かびます。そこで $n=8$ のグラフと 対数関数 $y=\log{x}+1.2$ を比較してみます。
 

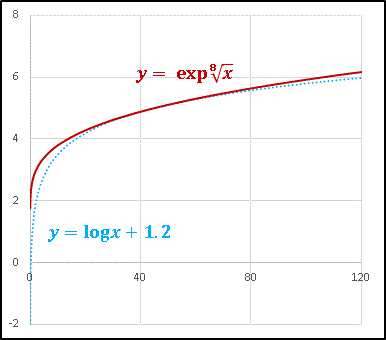
$[40,\ 60]$ のあたりでグラフは重なります。具体的には $x=50$ で差分は $\delta y=0.005$ 程度です。部分的にとはいえ、指数関数を使って対数関数のような曲線を作ることができるというのは、ちょっと面白いですね。

対称性を崩してみたり、三角関数を組込んでみたり

次は
 \[C(x) = \exp{f(x)}+\exp{g(x)}\]
という形の関数を扱います。まず最初に基本として $f(x)=x,\ g(x)=-x$ でグラフを描いてみると
 

 
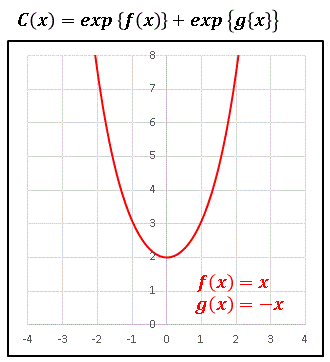
この曲線は 双曲線関数 の係数 $1/2$ を払った形、つまり
 \[y=2\cosh{x}=\exp(x)+\exp(-x)\]
のグラフです。$\cosh{x}$ をハイパボリック・コサインと呼びます。またこれは、カテナリー（懸垂線）と呼ばれる関数
 \[2y=\exp(ax)+\exp(-ax)\]
において $a=1$ とおいたものでもあります。いずれにしても指数関数を重ね合わせた奇関数ですから、左右対称のグラフとなります。たとえば $f(x)=x/2,\:g(x)=-x$ としてみると …
 

このように奇関数ではなくなって対称性は崩れてしまいます。$g(x)$ のほうが強く効くので、カテナリーを全体的に右下へ押し下げたような形になります。次に $f(x)=\cos{x},\:g(x)=-\sin{x}$ としてみると …
 

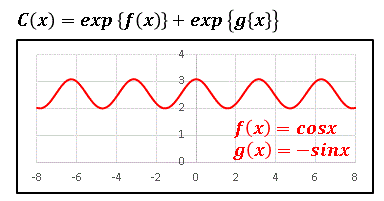
これは完全な周期関数です。$\exp{f(x)}\geq 1$ なので、$C(x)\geq 2$ となります。次は $f(x)=x+\cos{x},\:g(x)=-x-\sin{x}$ としてみます。
 

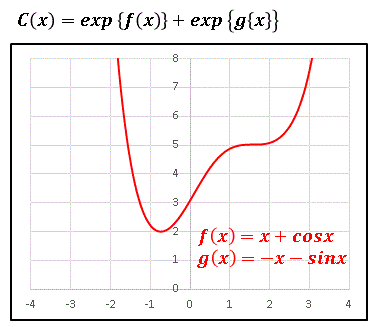
三角関数が効くのは原点付近だけで、$x$ が十分に大きいところでは $2\cosh{x}$ に一致します。