【算数問題32】植木算の基本問題
(1) 100 m の道路に端から端まで 5 m 間隔で木を植えるとき、何本の木が必要ですか?
(2) 互いに 60 m 離れた電柱と電柱の間に 5 m 間隔で木を植えます。何本の木が必要になりますか?
【ヒント】算数では定番の植木算です。こういう問題はとにかく絵を描いてみることです。でもあまりたくさんの木を描くのは大変ですから、自分で距離や間隔を適当に小さく設定してみましょう。
【解答の準備】下図のように、両端の間の距離を 5 m 、間隔を 1 m としたらどうなるのか考えてみましょう。
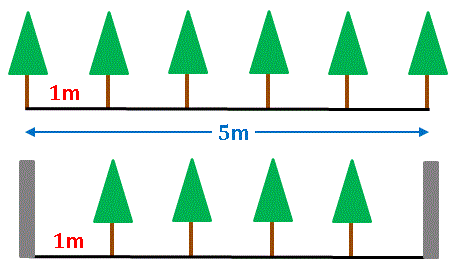
両端にも木を植える場合は 6 本、両端に電柱がある場合は 4 本ですね。電柱があってもなくても間隔の数 (5 つ) は一緒です。間隔の数と木の本数の関係を考えてみると、
両端に木を植える:木の数 = 間隔の数 + 1
両端に木を植えない:木の数 = 間隔の数 – 1
となっています。それでは解答に移りましょう。
【解答】(1) 間隔の数を計算すると
間隔の数 = 100 m ÷ 5 m = 20
ですから答えは
木の数 = 間隔の数 + 1 = 20 + 1 = 21 本
となります。
(2) 間隔の数は
間隔の数 = 60 m ÷ 5 m = 12
となるので、
木の数 = 間隔の数 – 1 = 12 – 1 = 11 本
が正解となります。
≫ [算数問題33] 本を出版します

エクセルや数学に関するコメントをお寄せください