包除原理・不等式による絞り込み

【NT04】二進数表記

$k$ 進数で表された数値 $x$ を $(x)_{k}$ と書くことにします。
(1) $(7.25)_{10}$ を $2$ 進数で表してください。
(2) $(7.2)_{10}$ を $2$ 進数で小数点以下 $7$ 桁まで表してください。
必要なら電卓を使ってください。
 
≫ 整数の k 進数展開についてはこちらの記事を参照してください。
 
【ヒント】$2$ 進数は $2$ ごとに繰り上がる $1$ と $0$ のみで表される数字です。$10$ 進数の整数 $0,\ 1,\ 2,\ 3,\ 4$ は 2 進数ではそれぞれ
 \[0,\ 1,\ 10,\ 11,\ 100\]
のように表されます。 $10$ 進数 $N$ を
 \[N=d_n 2^n+d_{n-1} 2^{n-1}+\ \cdots\ +d_1 2^1+d_02^0\]
と表したときの係数 $d_n$ が各桁を表すことになります：
 \[\begin{align*}&(0)_{10}=0\times 2^0\ \Longrightarrow\ (0)_2\\[6pt]&(1)_{10}=1\times 2^1\ \Longrightarrow\ (1)_{2}\\[6pt]&(2)_{10}=1\times 2^1+0\times 2^0\ \Longrightarrow\ (10)_2\\[6pt]&(3)_{10}=1\times 2^0+1\times 2^0\ \Longrightarrow\ (11)_2\\[6pt]&(4)_{10}=1\times 2^2+0\times 2^1+0\times 2^0\ \Longrightarrow\ (100)_2\end{align*}\]
整数ならそれほど難しくないのですが、小数だとはたしてどうなるか … 実は (2) はかなりの難問です。
　【解答】(1) 最初に上の説明の通り $(7)_{10}$ を $2^n$ で表すと
 \[(7)_{10}=1\times 2^2+1\times 2^1+1\times 2^0=(111)_2\]
と表記されます。計算技術的には簡略化された方法が知られているので、記事の後半で紹介しておきます。

小数点以下は $\cfrac{1}{2^n}$ の項を作って表すことになります。
電卓などで $\cfrac{1}{2^n}$ の数値を予め並べておきます。
 \[\begin{align*}&\frac{1}{2}=0.5,\quad \frac{1}{4}=0.25,\quad \frac{1}{8}=0.125,\quad \frac{1}{16}=0.0625,\quad\frac{1}{32}=0.03125\\[6pt]&\frac{1}{64}=0.015625,\quad\frac{1}{128}=0.0078125,\quad\frac{1}{256}=0.0390625\end{align*}\]
すると $0.25$ は
 \[0.25=\frac{1}{4}=0\times\frac{1}{2^1}+1\times\frac{1}{2^2}=(0.01)_2\]
と表されます。したがって先の $7$ の $2$ 進数表示と合わせて
 \[(7.25)_{10}=(111.01)_2\]
と表されることがわかります。小数点以下についても簡略化された計算法がありますので、記事下の補足を読んでおいてください。

(2) $0.25$ は比較的すっきり表せましたが、$2$ 進数で $0.2$ という数字は相性が悪く、無限級数になってしまいます（これがコンピュータの浮動小数点数演算の誤差の原因となっています）。問題では小数点以下 $7$ 桁まで求めよとなっているので、(1) で並べた数字を使って近似値を計算します。
 
$0.2$ の中には $0.125$ が１つあるので、$\cfrac{1}{2^3}$ の位は $1$ です。
そして、$0.2$ から $0.125$ を引きます。
 \[0.2-0.125=0.075\]
したがって、$\cfrac{1}{2^3}$ の桁は $1$ となります。以降同じようにして各桁の数字を求めていきます。

　　$0.075 － 0.0625 = 0.0125$　　∴$\cfrac{1}{2^4}$ の桁は $1$
　　$0.0125 \lt 0.03125$　　∴$\cfrac{1}{2^5}$ の桁は $0$
　　$0.0125 \lt 0.015625$　　∴$\cfrac{1}{2^6}$ の桁は $0$
　　$0.0125-0.0078125$　　∴$\cfrac{1}{2^7}$ の桁は $1$
　
以上より、$(7.2)_{10}=(111.0011001)_2$ と近似できます。

【補足】10 進数から 2 進数への変換する手順についてまとめておきます。まず整数部分から。$6$ を例にとって計算してみます。$6$ を $2$ で割り、商が $0$ になるまで順に $2$ で割っていきます。

　　6/2 = 3　余り 0
　　3/2 = 1　余り 1
　　1/2 = 0　余り 1

　そして余りを下から順に並べて $(110)_2$ が得られます。小数点以下の数は整数なるまで順に小数部分に $2$ をかけていきます。そして掛け算の結果が $1$ 未満ならその桁は $0$, $1$ 以上ならその桁は $1$ となります。たとえば $10$ 進数で $0.25$ だと、

　　0.25 × 2 = 0.5　：　0　（小数点以下1位）
　　0.5 × 2 = 1　　 ：　1　（小数点以下2位）

となって、上から並べて $(0.01)_2$ となります。 $10$ 進数で $0.2$ ならば、

　　0.2×2 = 0.4　：　0　（小数点以下1位）
　　0.4 × 2 = 0.8　：　0　（小数点以下2位）
　　0.8 × 2 = 1.6　：　1　（小数点以下3位）
　　0.6 × 2 = 1.2　：　14　（小数点以下4位）
　　0.2 × 2 = 0.4　：　0　（小数点以下5位）

のように循環することが簡単にわかります：
　
\[(0.2)_{10}=(0.001100110011……)_2\]

【NT05】包除原理

(1) $1$ から $99$ までの整数のうち、$2,\ 3,\ 5$ のいずれの数でも割り切れない数はいくつありますか。
(2) $99!$ を素因数分解したとき素因数 $5$ はいくつ含まれますか。

【ヒント】「含む含まれない」を考える問題です。混乱したらベン図などを書いて整理してみてください。ガウス記号を用いるとすっきりとした答案を作成できます。$[N]$ は $N$ を超えない整数という意味です。たとえば $[10.5]=10$ です。小問 (2) は $99!$ を素因数分解したときの $5$ の指数を求める問題です。

【考え方】$1$ から $10$ まで数を並べて $3$ の倍数に○をつけてみます。

1, 2, ③, 4, 5, ⑥, 7, 8, ⑨, 10

　$3$ の倍数は $3$ つごとに現れますから、$1$ から $10$ までに含まれる $3$ の倍数は $10$ を $3$ で割って端数を切り捨てた数 $[10/3]$ に等しいことになります。以上のことをふまえて解答を作ります。
　
　
【解答】(1) $99$ から $2$ の倍数、$3$ の倍数、$5$ の倍数の個数を引いてみます。
　
\[99-\left[\frac{99}{2}\right]-\left[\frac{99}{3}\right]-\left[\frac{99}{5}\right]=99-49-33-19=-2\]
　「マイナスの数？　計算ミス？」と驚かれるかもしれませんが、引きすぎがあるということです。$2$ と $3$ の共通倍数、$2$ と $5$ の共通倍数、$3$ と $5$ の共通倍数を二重に引いてしまっているので、今度はそれを足して戻します。
　
\[-2+\left[\frac{99}{6}\right]+\left[\frac{99}{10}\right]+\left[\frac{99}{15}\right]=-2+16+9+6=29\]
　しかし今度は $2,\ 3,\ 5$ の共通倍数 $30$ を足し過ぎているので再度引きます。
　
\[29-\left[\frac{99}{30}\right]=29-3=26\]
　分かりにくいと思ったら、下のベン図を参照してください。

　

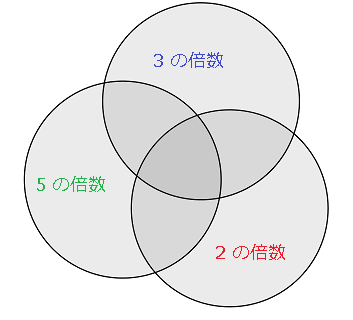
(2) $99!$ を書き下しておきます。
　
\[99!=1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdots 24\cdot 25\cdots 74\cdot 75\cdots 97\cdot 98\cdot 99\]
　素因数 $5$ は $5$ の倍数の中にしかないので、それを抜き出してみると
　
\[5,\ 10,\ 15,\ 20,\ 25,\ 30,\ 35,\ …,\ 70,\ 75,\ 80,\ …,\ 90, 95\]
　$25$ の倍数 $25,\ 50,\ 75$ には $5$ の倍数が $2$ つ含まれます。それ以外は $1$ つずつです。つまり $5$ の倍数について数え上げて、そのあと $25$ の倍数を数え上げて足せば、含まれる素因数 $5$ を過不足なく数えることができます。したがって、$99!$ に含まれる素因数 $5$ の数は
　
\[\left[\frac{99}{5}\right]+\left[\frac{99}{25}\right]=19+3=22\]
となります。

【NT06】分数式 4x/(2x^2+1) が整数となる条件

　次の分数式
\[f(x)=\frac{4x}{2x^{2}+1}\]が整数となるような実数 $x$ を求めてください。

【ヒント】二次方程式の問題に持ち込みます。
　
　
【解答】$n$ を整数として $f(x)=n$ とおくと次のような二次方程式が得られます。
　
\[2nx^2-4x+n=0\tag{1}\]
　$x$ は実数という条件があるので、判別式 $D/4\geq 0$ より
　
\[\frac{D}{4}=4-2n^2\geq 0\]
　これを解いて
　
\[n\leq 2\]
　$n$ は整数なので、
　
\[n=-1,\ 0,\ 1\tag{2}\]
となります。$n$ を含んだ形で二次方程式 (1) の解を表すと
　
\[x=\frac{2\pm \sqrt{4-2n^{2}})}{2n}\]
となります。$n=-1,\ 0,\ 1$ の値を代入すると、5 つの解
　
\[x=-1\pm\sqrt{2},\ 0,\ 1\pm\sqrt{2}\]
を得ます。

【NT07】不等式で絞り込みます

　分数式
\[f(n)=\frac{2n}{n^{2}+n+1}\]が整数となるような整数 $n$ を求めてください。

【ヒント】前回の問題に似ていますが、今回は整数解を求めます。
　
　
【解答】まず $n=0$ という解がすぐに見つかるので、以下では $n\neq 0$ として $0$ 以外の解を探します。$f(n)$ が整数であるためには分母が分子以下なくてはなりません。
　
\[n^2+n+1\neq |2n|\tag{1}\]
　絶対値記号を外して場合分けします。

[1] $n\gt 0$ のとき、
　
\[n^2+n+1\leq 2n\]
となります。左辺が $(\ \ )^2$ となるような形に変形して
　
\[\left(n-\frac{1}{2}\right)^2\leq-\frac{3}{4}\]
このような $n$ は存在しません。

[2] $n\lt 0$ のとき
　
\[n^2+n+1\leq -2n\]
左辺が $(\ \ )^2$ の形になるように変形すると、不等式
　
\[\left(n-\frac{3}{2}\right)^2\leq\frac{5}{4}\]
を得ます。これを解くと
　
\[-\sqrt{5}\leq 2n+3\leq\sqrt{5}\]
　$\sqrt{5}=2.236…$ であり、$2n+3$ は整数なので
　
\[-n\leq 2n+3\leq 2\]
　これを解いて
　
\[-2\leq n\leq -1\]
　したがって、$-2$ と $n=-1$ が解の候補となりますが、
　
\[f(-2)=-\frac{4}{3},\quad f(-1)=-2\]
なので、$n=-1$ が解です。以上より、$f(n)$ が整数となるような整数 $n$ は $0$ と $-1$ です。