二等辺三角形の面積を最大にする角度を求めます

算数問題62　二等辺三角形の面積を最大にする角度

　図のように AB と AC の長さが等しい二等辺三角形 ABC があります。この 二等辺三角形 ABC の面積を最大にする ∠BAC の大きさを求めてください。

　
　
　
　
　
　
　
　
　
【ヒント】パズルのような問題です。もちろん三角形の面積の公式を使って考えるのですが、問題文では具体的な辺の長さなどは一切与えられていません。つまり実際に計算する必要はないということです。実は二等辺三角形の面積は「円」と密接な関係があります。

素数に憑かれた人たち　リーマン予想への挑戦

解答62　AB を下にして考えます

　三角形の面積は

面積 = 底辺 × 高さ ÷ 2

で求められます。そこで問題図の三角形を横倒しにして底辺を AB とし、C から底辺 AB に下ろした垂線の長さを高さ h とします。

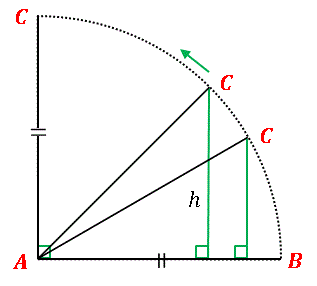
　AB はそのまま固定して C だけ動かすと、それに応じて高さ h も変化します。図にあるように ∠BAC が直角のとき、AC が三角形 ABC の高さ h となって、またこのとき h が最大となります。よって二等辺三角形を最大にするのは ∠BAC = 90°のときです。