正八角形と少なくとも１辺を共有する三角形を数えます

【算数問題61】正八角形と少なくとも１辺を共有する三角形

正八角形の 3 個の頂点を結んで三角形を作ります。このとき正八角形と少なくとも１辺を共有する三角形は全部でいくつありますか？
 
【ヒント】何はともあれ正八角形の図を描きましょう。きちんと図を描いてみれば意外と簡単な問題です。「少なくとも１辺を共有する」ということは …
　
【解答61】少なくとも１辺を共有するとあるので、２辺を共有する三角形も含みます。つまり下図のように２種類の三角形をかぞえればよいことになります。
 

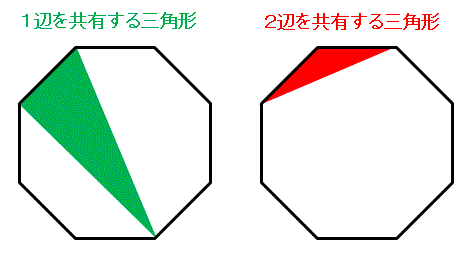
まず１辺を共有する緑色の三角形について考えてみます。ある１つの辺を選んだとします。３つめの頂点として、その辺の隣にある頂点は選べないので、それを除いた残る４つの頂点と結んで三角形をつくることになります。つまり１辺につき４つの緑色の三角形ができるので、全部で

8 × 4 = 32個

の三角形をつくることができます。次に２辺を共有する赤い三角形について考えると、これは頂点の数に等しく、つまり全部で８個の三角形があります。ですから三角形は全部で

32 + 8 = 40個

となります。
 
【補足】ついでに一般に n 角形の頂点を結んで作られる三角形もかぞえてみます（ただし n≧4）。数え方は上の解答とまったく同じです。１辺を共有する三角形は、１つの辺について、その辺を結ぶ２点と隣の２点をのぞいた４点を除いた数だけあるので、全部で

n(n-4)個

あります。２辺を共有する赤い三角形は頂点の数に等しいので n 個です。つまり全部で

n(n-4) + n = n(n-3)個　(n≧4)

あります。ここで n = 8 とすれば正八角形のときにつくられる三角形の数

n(n-3) = 8 × 5 = 40個

が得られます。