条件付き確率
ある事象 $A$ が起こったときに事象 $B$ が起こる確率を条件付き確率(conditional probability)とよび、$P(B|A)$ と表します。
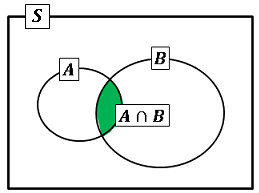
上図のように標本空間 $S$ の中に事象 $A,\:B$ を考えるとき、$P(B|A)$ は $A$ の中で事象 $A\cap B$ が起こる確率なので、
\[P(B|A)=\frac{n(A\cap B)}{n(A)}\]
と表すことができます。ここで
\[P(A)=\frac{n(A)}{n(S)},\quad P(A\cap B)=\frac{n(A\cap B)}{n(A)}\]
を代入すると
\[P(B|A)=\frac{n(A\cap B)}{n(S)}\frac{n(S)}{n(A)}=\frac{P(A\cap B)}{P(A)}\]
となるので、乗法定理
\[P(A\cap B)=P(A)P(B|A)\]
を得ます。この定理を言葉で書くと、
[A,Bが共に起こる確率] = [Aが起こる確率] × [Aが起こったときにBが起こる確率]
となります。乗法定理はより多くの事象を考える場合でも成り立ち、たとえば 3 つの事象 $A,\:B,\:C$ については
\[P(A\cap B\cap C)=P(A)P(B|A)P(C|A\cap B)\]
という式になります。
トランプから続けて2枚のスペードが引かれる確率
ジョーカーを除いた $52$ 枚のトランプのカードから続けて $2$ 枚引いて、$2$ 枚ともスペードである確率を計算してみます。事象を $A,\:B$ を次のように定義しておきます。
事象A:$1$ 枚目のカードがスペードである。
事象B:$2$ 枚目のカードがスペードである。
最初は $52$ 枚のカードから $1$ 枚を引くので
\[P(A)=\frac{13}{52}=\frac{1}{4}\]
であり、次は $51$ 枚のカードから $1$ 枚を引くので
\[P(B|A)=\frac{12}{51}=\frac{4}{17}\]
となります。$2$ 枚ともスペードになる確率は乗法定理を用いて
\[P(A\cap B)=P(A)P(B|A)=\frac{12}{51}\frac{4}{17}=\frac{1}{17}\]
と計算することができます。
事象の独立性
ジョーカーを除いた $52$ 枚のトランプのカードから $1$ 枚を引いて、それを戻してよくシャッフルし、もう一度カードを引きます。このとき $2$ 枚ともスペードである確率を計算してみます。事象を $A,\:B$ を次のように定義しておきます。
事象A:$1$ 枚目のカードがスペードである。
事象B:$2$ 枚目のカードがスペードである。
最初は $52$ 枚のカードから $1$ 枚を引くので
\[P(A)=\frac{13}{52}=\frac{1}{4}\]
となります。そして次もまた $52$ 枚のカードから $1$ 枚を引くので
\[P(B|A)=\frac{13}{52}=\frac{1}{4}\]
となります。よって乗法定理より
\[P(A\cap B)=P(A)P(B|A)=\frac{1}{4}\frac{1}{4}=\frac{1}{16}\]
と計算することができます。先ほどの例と異なって、2回目にカードを引くときにスペードである確率は、(カードの総数が変わらないので)1回目の結果がどのようなものであろうと影響を受けていません。すなわち
\[P(B|A)=P(B)\]
が成り立っていて、乗法定理は
\[P(A\cap B)=P(A)P(B)\]
という簡単な式で表されます。このように2つの事象 $A,\:B$ があって、一方の事象が起こることが、他方の事象が起こることに影響を与えないとき、事象 $A$ と $B$ は独立 (independent)であるといいます。また事象 $A$ と $B$ がでないときは、事象 $A$ と $B$ は従属(dependent)であるといいます。

エクセルや数学に関するコメントをお寄せください