伝染理論と伝染曲線

【DE06】伝染曲線 (感染者の増加率)

人口 $N$ 人の都市で伝染病が発生したとします。ある時刻において、まだ感染していない人の数を $x(t)$ とし、未感染者が感染者が接触した時に伝染がおこるとします。すなわち単位時間当たりの感染者の増加数は $x(N-x)$ に比例すると考えます。ただし $t=0$ における感染者は 1 名とします。このようなモデルにおいて、
(1) 未感染者の数 $x(t)$ を求めてください。
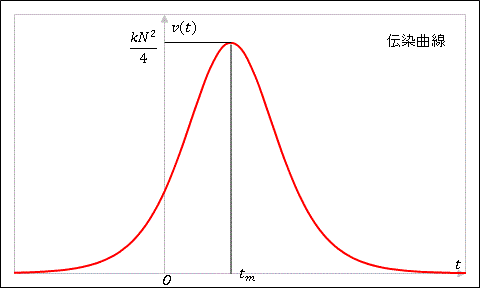
(2) ある時刻における感染者の増加率 $v(t)=-dx/dt$ のグラフ（伝染曲線）を描いてください。

【ヒント】(1) は微分方程式を立てて解く問題。(2) は極値を調べてグラフ (伝染曲線) を描く問題です。増加率 $v(t)$ の微分は、小問 (1) で立てた微分方程式を利用するととても楽になります。また、実際にグラフを描く前に、状況から概形を予想してみてください。
　
【解答】$k$ を定数とすると感染者の増加率は
 \[kx(N-x)\]
ですが、求めたいのは未感染者の数なので符号を反転させて
 \[\frac{dx}{dt}=kx(x-N)\tag{A}\]
と表せます。変数分離すると
 \[\frac{dx}{x(x-N)}=kdt\]
左辺の分数を分解すると
 \[\left(\frac{1}{x-N}-\frac{1}{x}\right)dx=Nkdt\]
積分すると
 \[\log\left|\frac{x-N}{x}\right|=Nkt\]
$A=\pm e^c$ とおくと
 \[x=\frac{N}{1-Ae^{Nkt}}\]
$t=0$ で「未感染者の数」は $x=N-1$ なので、上の式に代入して定数 $A$ を求めると
 \[A=\frac{1}{1-N}\]
となります。よって未感染者の数
 \[x(t)=\frac{N(N-1)}{N-1+e^{Nkt}}\tag{A1}\]
が得られます。

(2) 時刻 $t=0$ から感染者の増加率は徐々に増して、ある一定のピークを迎えたのち、今度は減少に転じて最後は 0 になるはずです（全員が感染したら増加率は 0 になるはずです）。したがって $v(t)$ はある時刻 $t=t_m$ で極大値を１つもち、$t\rightarrow \infty$ で 0 に収束するような関数であると予測できます。実際に確かめてみましょう。
 \[v(t)=-\frac{dx}{dt}=-kx(x-N)\tag{B}\]
に (A1) を代入すると
 \[v(t)=\frac{kN^2(N-1)e^{Nkt}}{N-1+e^{Nkt}}\tag{B1}\]
となります。状況から考えても、またこの関数の形からも常に $v(t)\gt 0$ であることがわかります。さて極値を求めるために $v(t)$ を微分しますが、それには (B) の表式を用いると簡単です。すなわち
 \[\frac{dv}{dt}=-kx'(x-N)-kxx’=kx'(N-2x)=-v(t)(N-2x)\]
となります。$v(t)\gt 0$ なので、$v'(t)=0$ となるのは $x=N/2$ のときです。これを先ほどの
 \[x(t)=\frac{N(N-1)}{N-1+e^{Nkt}}\tag{A1}\]
に入れると極値をとる時刻 $t_m$ が求まります。
 \[t_m=\frac{\log(N-1)}{Nk}\]
(B1) に代入すると極値が求まります。
 \[v(t_m)=\frac{kN^2}{4}\gt 0\]
$t\rightarrow \pm\infty$ で $v(t)=0$ となること、常に $v(t)\gt 0$ であること、また極値 $v(t_m)$ も正であることから、$v(t_m)$ は極大値であることがわかります。グラフの概形は下の図のようになります。
 

【DE07】非線形方程式

微分方程式 $xy’-y+xe^xy^3=0$ を解いてください。
 
【ヒント】非線形方程式ですが、上手く変数変換すると線形方程式に帰着できます。詳しくは ベルヌーイの微分方程式の頁を参照してください。

【解答】与えられた方程式
 \[xy’-y+xe^xy^3=0\tag{A}\]
の両辺を $y^3$ で割ります。
 \[x\frac{y’}{y^3}-\frac{1}{y^2}+xe^x=0\]
$(y-2)’=-2y’y^{-3}$ なので
 \[\frac{x}{2}+\left(\frac{1}{y^2}\right)=xe^x\]
ここで $z=1/y^2$ とおくと
 \[xz’+2z=2xe^x\tag{A1}\]
という方程式になります。右辺を 0 とおいた斉次方程式
 \[xw’+2w=0\]
を変数分離すると
 \[\frac{dw}{w}=-2\frac{dx}{x}\]
両辺を積分すると
 \[\log|w|=-\log x^2+c\]
$A=\pm e^c$ とおくと
 \[w=\frac{A}{x^2}\]
という斉次解を得ます。そこで $z=a(x)/x^2$ とおいて先ほどの
 \[xz’+2z=2xe^x\tag{A1}\]
に代入すると $a(x)$ に関する方程式
 \[a'(x)=2x^2e^x\]
が得られます。積分公式
 \[\int f(x)e^xdx=\{f(x)-f'(x)+f^{\prime\prime}(x)-\cdots\}e^x\]
と用いて積分すると
 \[a(x)=(2x^2-4x+4)e^x+c\]
となるので、
 \[z=\frac{(2x^2-4x+4)e^x+c}{x^2}\]
となります。よって
 \[y^2=\frac{x^2}{(2x^2-4x+4)e^x+c}\]
という一般解を得ます。