[EX01] 3604990 と 92631 の最大公約数
(1) 3604990 と 92631 の最大公約数を求めてください。
(2) 72, 544, 1168 の最小公倍数を求めてください。
【ヒント】最大公約数と最小公倍数のことを英語でそれぞれ Greatest Common Divisor,Least Common Multiple といいます。
新品価格 |  |
【解答】(1) 最大公約数がほしいときは GCD 関数を使います。セルに
=GCD(3604990,92631)
と入力すれば 3604990 と 92631 の最大公約数 401 が得られます。ちなみに手計算でやる場合はユークリッド互除法を用いますが、かなり面倒です。
(2) 数値群の最小公倍数は LCM 関数 によって得られます。セルに
=LCM(72,544,1168)
と入力すれば 72, 544, 1168 の最小公倍数 357408 が返ってきます。
[EX02] sin19°とcos(55°)^3の値を求めます
(1) $\sin 19^{\circ}$ の値を求めてください。
(2) $\cos^{3} 55^{\circ}$ の値を求めてください。
ただし、いずれも小数点以下 3 桁で答えるものとします。
【ヒント】引数の単位に注意です！
新品価格 |  |
【解答】Excel には $\sin x,\:\cos x\:\tan x$ の値を返す SIN, COS, TAN という関数が用意されていますが、その引数はラジアン単位で入れることになっています。そこで RADIANS関数によって引数の「度」を「ラジアン」に変換しておく必要があります。
(1) $\sin 19^{\circ}$ は
=SIN(RADIANS(19))
と入力して 0.326 が得られます。
(2) べき乗は「^」という演算子を使います。$\cos^3 55^{\circ}$ は
=COS(RADIANS(55))^3
と入力して 0.189 が得られます。
[EX03] 係数の大きな二次方程式の解
二次方程式 $133x^2-3531x+23436=0$ を解いてください。ただし、解は分数の形で表してください。
【ヒント】解は有理数です。まとめて計算させようとすると入力ミスなどを生じやすいので、係数を別々のセルに入れて処理しましょう。
数学 図形と関数・グラフの融合問題 完全攻略272選 (高校入試特訓シリーズ) 新品価格 |  |
【解答】二次方程式の解の公式
\[x=\frac{-b\pm\sqrt{D}}{2a},\quad D=b^2-4ac\]を用いて解を求めます。次のようなシートを作ってみます。
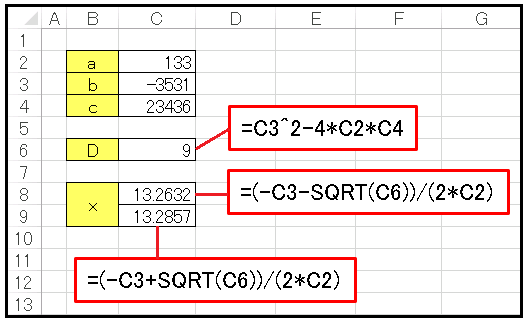
セル C2, C3, C4 に係数 $a,\:b,\:c$ を入れておきます。
セル C6 で判別式 $D$ の値を計算させます：
=C3^2-4*C2*C4
セル C8 と C9 にはそれぞれ
=(-C3-SQRT(C6))/(2*C2) =(-C3+SQRT(C6))/(2*C2)
と入力して 2 つの解を計算させます。ただし、初期設定では値が小数で表示されるので、これを分数表示に変えます。セル C8 と C9 を選択した状態で [ホーム] ⇒ [表示形式] ⇒ [その他の設定] の順に選択します（あるいは右クリック ⇒ [セルの書式設定]）。すると次のような画面が現れます。
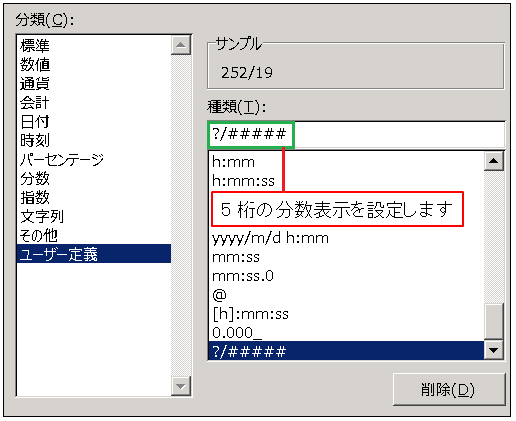
この画面で [ユーザー定義] を選択し、[種類] のテキストボックスに
?/#####
と書きこんでおきます（ # は桁数を表すので適当に多めに入れておきます）。
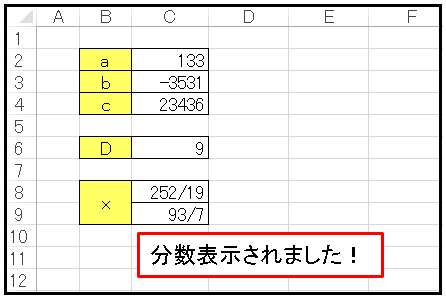
分数表示されましたね。よって 2 解が
\[x=\frac{252}{19},\quad\frac{93}{7}\]であることがわかりました。
[EX04] Excelで条件を満たす整数を求めます
$f(n)=[n^\sqrt{n}]$ が 3 桁の数字となるような自然数 $n$ を全て求めてください。ここで $[x]$ は $x$ を超えない最大の整数を表すものとします。
【ヒント】$n$ と $f(n)$ のデータを作って確認します。
新品価格 | |
【解答】下図のようなワークシートを作ります。
A 列に $n$ を適当な数だけ並べておきます。$\sqrt{n}$ は SQRT関数で計算させます。また $[x]$ は指定された数値を最も近い整数に切り捨てる INT関数を用います。ですからセル B1 に
=INT(A2^SQRT(A2))
と入力して $f(1)$ を計算させ、A11 までオートフィルして $f(n)$ のデータを埋めます。すると $n=7,\:8,\:9$ で 3 桁の数字になっていることがわかります。
[EX05] 絶対値を含む方程式 |x-2|+|x^2-4|=x/4+5 の解の個数
方程式 $\displaystyle |x-2|+|x^2-4|=\frac{x}{4}+5$ を満たす解の個数を求めてください。
【ヒント】目で見て交点を数えればよいのです。
新品価格 |  |
【解答】解の個数を問われているので、$y=|x-2|+|x^2-4|$ と $y=x/4+5$ のグラフを描いて交点の数をかぞえればよいのです。$x$ を 0.1 刻みで -4 ～ 4 ぐらいの範囲で設定して、次のようなワークシートを作ります。
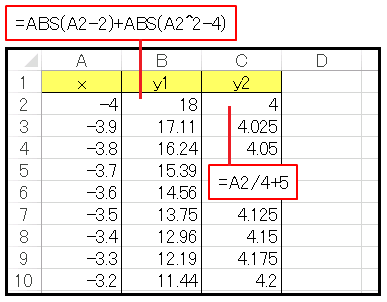
数値の絶対値を求めるときは ABS 関数を用います。セル B2 と C2 にはそれぞれ
=ABS(A2-2)+ABS(A2^2-4) =A2/4+5
と入力し、B2 と C2 を同時選択して C2 の右下隅をダブルクリックすると列にデータが埋まります。次は A 列から C 列まで同時選択して、[ホーム] ⇒ [散布図] ⇒ [散布図（平滑線）] の順にクリックすると、グラフが表示されるので、軸や目盛などを適当に設定します。
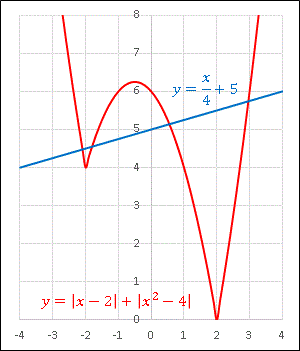
グラフの交点を数えると「解が 4 個ある」ことがわかります。
エクセルや数学に関するコメントをお寄せください