放物線上の接線と法線

【CL17】放物線上の接線と法線

放物線 $y=x^2$ 上の１点 $R$ に接線と法線を引きます。
 

 
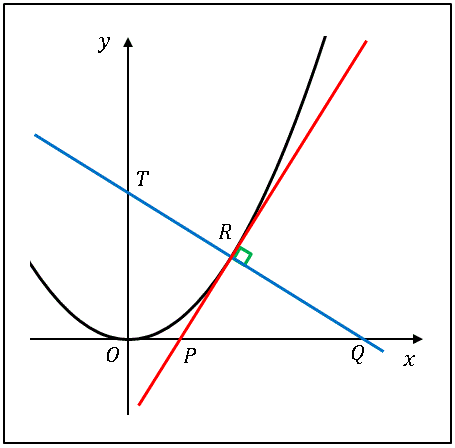
図のように、接線（赤い線）が $x$ 軸と交わる点を $P$ とし、法線（青い線）が $x$ 軸と交わる点を $Q$, $y$ 軸と交わる点を $T$ とします。このとき △$PQR$ の面積 $S_1$ が △$OQT$ の面積 $S_2$ のちょうど半分となるように点 $R$ の座標を定めてください。
 
【ヒント】接線と法線の方程式を立てます。
　
【解答】放物線上の点 $R$ を $(a,\:a^2)$ とします。$y=x^2$ を微分すると $y’=2x$ なので、点 $R$ における接線の方程式は
 \[y-a^2=2a(x-a)\]
と書くことができます。\(y=0\) とおいて $x$ 軸との交点 $P$ の $x$ 座標を求めると
 \[x=\frac{a}{2}\]
となります。法線の方程式は
 \[y-a^2=-\frac{1}{2a}(x-a)\]
となります。$y = 0$ とおくと、 $x$ 軸との交点 $Q$ の $x$ 座標は
 \[x=2a^3+a\]
であり、また $x=0$ とおいて、$y$ 軸との交点 $T$ の $y$ 座標を
 \[y=a^2+\frac{1}{2}\]
と求めることができます。
 

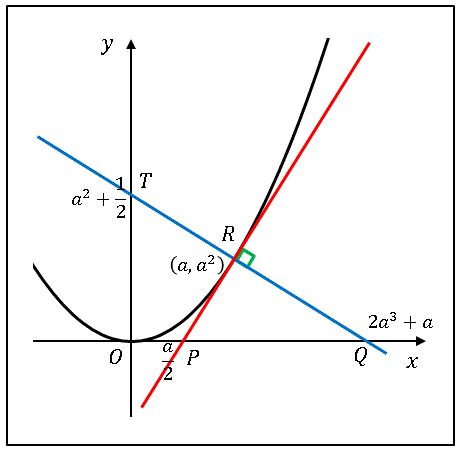
以上より △$PQR$ の面積 $S_1$ は
 \[S_1=\frac{1}{2}a^2 \left( 2a^3+a-\frac{a}{2} \right) =\frac{1}{4}a^3(4a^2+1)\]
となります。また、△$OQT$ の面積 $S_2$ は
 \[S_2=\frac{1}{2}(2a^3+a)\left( a^2+\frac{1}{2}\right)=\frac{1}{4}a(2a^2+1)^2\]
となります。 \(S_1=S_2/2\) とおくと
 \[4a^4-2a^2-1=0\]
という方程式が得られるので、$a^2\gt 0$ となる解を求めると
 \[a^2=\frac{1+\sqrt{5}}{4}\]
が得られます。よって点 $R$ の座標は
 \[(x,\:y)= \left(\sqrt{\frac{1+\sqrt{5}}{4}},\:\frac{1+\sqrt{5}}{4} \right),\:\left(-\sqrt{\frac{1+\sqrt{5}}{4}},\:\frac{1+\sqrt{5}}{4}\right)\]
となります。