集合の演算（交換・結合・分配）

集合の定義（有限集合と無限集合）

たとえば「8 以下の自然数」を書き並べて
 $$1,2,3,4,5,6,7,8$$
のように範囲が定まった集まりをつくります。このような集まりのことを 集合 (set) とよびます。そして集合を構成している個々のものを 要素 (element) といいます。全ての要素を { } で括って
 $$A=\{1,2,3,4,5,6,7,8\}$$
のように書けば、$A$ は「8 以下の自然数」で構成される集合であることを明示したことになります。この例のように要素の数が有限であるとき、この集合を有限集合とよびます。しかし、たとえば自然数全体を集合として扱う場合は、要素数が無限にあるため無限集合とよび、
 $$A=\{1,2,3,\cdots \}$$
のように表します。

部分集合と真部分集合

集合を考えるときは下の図のような ベン図 (Venn diagram) を用いて表すと複雑な関係も理解しやすくなります。
 

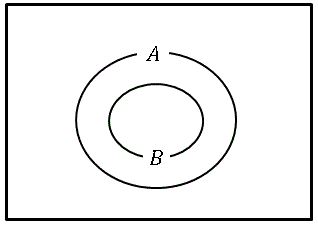
図にあるように、集合 $A$ のどの要素も集合 $B$ の要素であるときには、$A$ は $B$ の 部分集合 (subset) であるといい、
 $$A\subseteq B$$
という記号で表します。たとえば正の偶数全体は自然数の部分集合となります。この記号は $A$ と $B$ の要素が全て一致している場合も表しています。$A\subseteq B$ かつ $B\subseteq A$ ならば、$A$ と $B$ の要素は一致しているといい、
 $$A=B$$
と表します。もし $A$ と $B$ が等しくないことが明らかな場合は
 $$A\subset B$$
と書いて、$A$ は $B$ の真部分集合 (proper subset) であるといいます。

共通部分と和集合

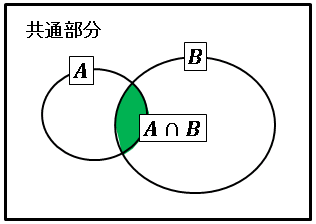
下図のように、$A$ と $B$ のどちらにも含まれる要素で構成される集合のことを $A$ と $B$ の共通部分 (intersection) とよび、
 $$A\cap B$$
と表します。「$A$ かつ $B$」あるいは「$A$ cap $B$」と読みます。
 

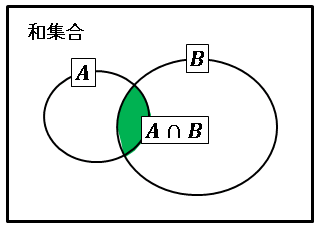
$A$ と $B$ の少なくとも一方に含まれる要素で構成される集合のことを $A$ と $B$ の 和集合 (union) とよび、
 $$A\cup B$$
と表します。「$A$ または $B$」あるいは「$A$ cup $B$」と読みます。
 

全体集合と補集合、空集合

最初にある１つの集合 $U$ を定義して、$U$ の要素や部分集合を考えるとき、$U$ を 全体集合 (universe) といいます。$U$ の部分集合 $A$ を定義したとき、$A$ に属していない要素で構成される集合を $A$ の補集合とよび、$\overline{A}$ で表します。
 

 
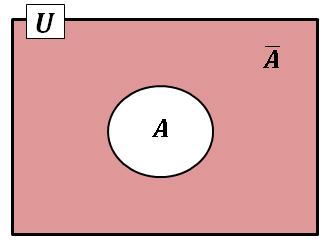
また、要素を１つも含まない集合のことを 空集合 (null set) とよび $\varphi$ で表します。

集合の演算

集合の演算規則についてまとめておきます。
 $$\begin{array}{rl}\overline{A}& =A\\ A\cap \overline{A}& =\varphi \\ A\cup U& =U\\ A\cap U& =A\end{array}$$
① 交換法則
$$\begin{array}{r}A\cup B=B\cup A\\ A\cap B=B\cap A\end{array}$$② 結合法則
$$\begin{array}{r}A\cup (B\cup C)=(A\cup B)\cup C\\ A\cap (B\cap C)=(A\cap B)\cap C\end{array}$$③ 分配法則
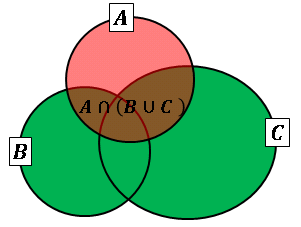
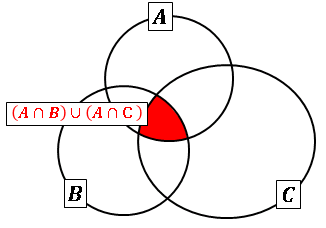
$$\begin{array}{r}A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\\ A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\end{array}$$④ ド・モルガンの法則
$$\begin{array}{r}\overline{A\cap B}=\overline{A}\cup \overline{B}\\ \overline{A\cup B}=\overline{A}\cap \overline{B}\end{array}$$
下のベン図は分配法則を表したものです。
 

 

集合の和

有限集合 $A$ に対して、その要素の数を $n(A)$ と書くと、2 つの有限集合 $A,B$ の要素の数について次の式が成り立ちます。
 $$n(A\cup B)=n(A)+n(B)-n(A\cap B)$$
$n(A)+n(B)$ は共通部分を重複して数えているので、そのぶんだけ 1 回引いておくのです。たとえば $A,B$ を
 $$A=\{2,4,6,8,10,12\},B=\{3,6,9,12\}$$
のように定義して、この 2 つの集合を合わせることを考えます。それぞれの要素の数を単純に足し合わせると
 $$n(A)+n(B)=6+4=10$$
となりますが、共通部分の 6 と 12 を余分に数えているので、それを差し引いて
 $$n(A\cup B)=n(A)+n(B)-n(A\cap B)=10-2=8$$
となります。$A\cap B=\varphi$ のときは共通部分がないので
 $$n(A\cup B)=n(A)+n(B)$$となります。

集合の積

2 つの集合 $A,B$ について、1 つずつ要素 $a,b$ を取り出して $a$ のあとに $b$ を並べたものを 順序対 とよび、$(a,b)$ で表します。集合 $A,B$ に含まれるすべての要素について順序対をつくり、それらを全て含む集合を $A$ と $B$ の 直積 (direct product) とよび、
 $$A\times B=\{(a,b)|a\in A,b\in B\}$$
で表します。たとえば
 $$A=\{1,2,3\},B=\{4,5\}$$
と定義すると
 $$A\times B=\{(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)\}$$
となります。$A$ の要素 1 つに対して $B$ の要素が 2 つあるので、直積集合の数は 3 × 2 = 6 個となっています。一般に直積集合の数は
 $$n(A\times B)=n(A)\times n(B)$$
によって計算できます。