算数問題の代表選手（？）つるかめ算を解きましょう

　算数といえば、やっぱり つるかめ算。
　大人でもけっこう苦手な人が多いようです。
　算数なので方程式を使うのは禁止です！　真向勝負で解いてくださいな。

【算数問題02】つるさんとかめさん、それぞれいくつ？

　つるとかめが合わせて 10 で、足数の合計は 26 本です。つるとかめは、それぞれいくついますか？

【ヒント】全体の差 を使う有名な解き方と、ちょー簡単な方法がありますよ。
　え？　「ちょー簡単な方法」を教えてほしい？　それは解答を見てのお楽しみです♪

【解答①】つるかめ算の基本的な考え方 に沿って解いていきます。
　下図を参照しながら解説を読んでください。

　

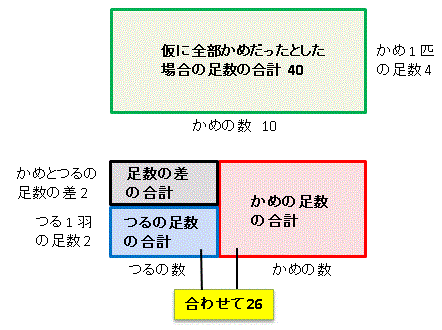
　とりあえず「全部かめだったら足数の合計は 40 本だね」と考えます。
　それを図にすると、縦を「かめの足数 4 」、横を「（仮の）かめの数 10 」とした緑色の長方形の面積に相当します。でも実際には全部かめのはずはないので、その下にあるように「つるの足数の合計」を示す青い長方形と「かめの足数の合計」を示す赤い長方形の合わさった L 字型図形になっているはずです。その合計は問題文に 26 と与えられていますね。
　そして先ほどの大きな長方形の面積 40 から、この L 字型図形の面積 26 を引いた灰色部分に注目すると、その面積は
　
\[足数の差の合計（全体の差）=40-26 = 14\]
となっていますね。これは横が「つるの数」、縦が「かめとつるの足数の差」ですから、「かめとつるの足数の差 = 2 」で割ると「つるの数」が得られるという仕組みになっています。
　
\[つるの数=足数の差の合計\div かめとつるの足数の差=14\div 2=7\]
ですから、かめの数は
　
\[かめの数=10-7=3\]
となります。
　
【解答②】それではお待たせしました。ちょー簡単な解き方です。かめの足の総数は 4 の倍数、つるの足の総数は 2 の倍数になっているはずです。ということは、つるとかめの足数の合計 26 を 4 の倍数と 2 の倍数の足し算で表せばよいのです。（　　）の中に分けた数字を 4 と 2 で割った数字（それぞれ、かめとつるの数です）とその合計が示されています。
　
\[\begin{align*}&26=4+22\quad(かめ1匹、つる11羽\quad合計12)\\[6pt]
&26=8+18\quad(かめ2匹、つる9羽\quad 合計11)\\[6pt]
&26=12+14\quad(かめ3匹、つる7羽\quad 合計10)\end{align*}\]
　はい。つるとかめの合計がちょうど 10 になりましたので、かめ 3 匹、つる 7 羽が正解です。

　かめ 1 匹という正解はあまりなさそうだと考えて、26 = 8 + 18 から始めるともっと早く答えがでますよ。暗算が得意な人は頭の中で割り算しながらいきなり 26 = 12 + 14 を見つけることもさほど難しくありません。文字通り「つるとかめ」が登場する問題では必ず 4 の倍数と 2 の倍数を使うので、ほとんどこの方法で解けますが、「買い物問題」など、もう少し数字が大きくなると倍数の足し算を見つけることが面倒な場合もあります。でも心配ご無用！　次回、ほとんどの問題で通用する「つるかめ算」の解法を紹介する予定です。