階乗の定義と計算方法
正の整数 $n$ について
\[n!=\begin{cases}n\,(n-1)\,(n-2) \cdots 2 \cdot 1 & (n\neq 0)\\[6pt]
1 & (n=0)\end{cases}\]
を $n$ の階乗(factorial)と定義します。たとえば、
\[\begin{align*}3!=&\,3 \cdot 2 \cdot 1=6\\[6pt]5!=&\,5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\end{align*}\]
のように計算します。階乗は数学のあらゆる場面で登場します。特に確率論による組合せや オイラー積分(ガンマ関数)、関数の級数展開などの計算で活躍します。
コンピュータで階乗を計算させるには再帰的定義を用いると簡単です。
\[n!=\begin{cases}1 & (n=0)\\[6pt]n(n-1)! & (n\geq 1)\end{cases}\tag{2}\]
つまり $n = 0$ の場合だけ特別に $0! = 1$ の値を与えて、$n \gt 1$ については For文などのループ処理で
\[\begin{align*}1!=&1\\[6pt]2!=&2 \cdot 1!=2\\[6pt]3!=&3 \cdot 2!=6\\[6pt]4!=&4 \cdot 3!=24\end{align*}\]
といった具合に計算させます。
$x^n$ の導関数で階乗を定義することもできます。たとえば $x^3$ を順に微分していくと、
\[\begin{align*}&\frac{d(x^3)}{dx}=3x^2\\[6pt]&\frac{d^2(x^3)}{dx^2}=3 \cdot 2x\\[6pt]&\frac{d^3(x^3)}{dx^3}=3 \cdot 2 \cdot 1=3!\end{align*}\]
となります。一般に階乗は $x^n$ の n階微分によって
\[n!=\frac{d^n}{dx^n}\,x^n\tag{3}\]
と定義することができます。
【Excel】FACT関数
Excel の FACT(x) は x の階乗を返します。たとえば、セルに
=FACT(10)
と入力すると、$10!$ を計算して 3628800 を返します。階乗の定義にしたがって、FACT(0) は 1 を返します。FACT に負数を渡すとエラーとなります。たとえば、
=FACT(-5)
と入力すると、#NUM! すなわち関数に無効な数値が渡されたことを示すエラーが表示されます。数学では階乗は非負の整数のみに定義されていますが、FACT に小数を渡してもエラーとはなりません。引数の小数部は切り捨てられ、整数部の階乗を返します。たとえば、
=FACT(4.8)
と入力した場合、4 の階乗を計算して 24 を返します。
スターリングの公式
スターリングの公式
\[\Gamma (x+1)\sim \sqrt{2\pi x}x^xe^{-x}\tag{4}\]
を用いると、階乗についての近似式
\[\Gamma (n+1)=n!\sim \sqrt{2\pi n}\left ( \frac{n}{e} \right )^n\tag{5}\]
を得ます。この近似は $n$ が大きな値をとるほど精度がよくなります。
二重階乗の定義と計算方法
正の整数 n について、
\[n!!=\begin{cases}n\,(n-2)\,(n-4) \cdots 3 \cdot 1 & (n=\mathrm{odd\ number})\\[6pt]
n\,(n-2)\,(n-4) \cdots 4 \cdot 2 & (n=\mathrm{even\ number})\\[6pt]
1 & (n=0\ \mathrm{or}\ -1)\end{cases}\tag{6}\]
を n の二重階乗(double factorial)と定義します。たとえば、
\[7!!=7 \cdot 5 \cdot 3 \cdot 1=105\]
のように計算します。二重階乗はガンマ関数やベッセル関数など特殊関数の計算などで用います。二重階乗は普通の階乗と指数の組合せで表すこともできます。
\[(2m)!!=2^m m!, \qquad (2m-1)!!=\frac{(2m)!}{2^m m!}\tag{7}\]
証明は簡単です:
\[\begin{align*}(2m)!!=&2m\,(2m-2)\,(2m-4) \cdots 4 \cdot 2\\[6pt]=&2^m\,m\,(m-1)\,(m-2) \cdots 2 \cdot 1=2^m m!\end{align*}\tag{8}\]
また、$(2m)!!=2^m m!$ の両辺に (2m – 1)!! をかけると、
\[(2m)!!(2m – 1)!!=2^m m!(2m – 1)!!\tag{9}\]
左辺は $(2m)!$ となるので、
\[(2m)!=2^m m!(2m – 1)!!\tag{10}\]
したがって、
\[(2m-1)!!=\frac{(2m)!}{2^m m!}\tag{11}\]
が証明されました。たとえば、$m=4$ としてみると、
\[7!!=\frac{8!}{2^44!}=\frac{8\cdot 7\cdot 6\cdot 5}{16}=105\tag{12}\]
となります。
【Excel】FACTDOUBLE関数
Excel の FACTDOUBLE(x) は x の二重階乗を返します。たとえば、
=FACTDOUBLE(8)
と入力すると、$8!!=8\cdot 6\cdot 4\cdot 2$ を計算して 384 を返します。FACTDOUBLE(0) および FACTDOUBLE(1) は 1 を返します。FACTDOUBLE に負数を渡すと、無効な数値が渡されたことを示す #NUM! を返します。FACTDOUBLE に小数を渡した場合、小数部は無視されて、整数部の二重階乗を返します。たとえば、あるセルに
=FACT(5.5)
を入力すると、5 の二重階乗 $5!!=5\cdot 3\cdot 1$ を計算して 15 を返します。
【EX14】Excel で階乗を含む級数を計算します
Excel を用いて次の級数
\[S=\sum_{k=1}^{10}\frac{k-1}{k!}\]の値を計算して小数点以下 8 桁まで表示させてください。
【ヒント】基本問題ですが、階乗計算の関数を使う必要があります。
【解答】数値の階乗を計算するときは FACT関数を使います。たとえば次のようなシートを作って、セル C3 には
=(B3-1)/FACT(B3)
と入力してセル C12 までコピーします。
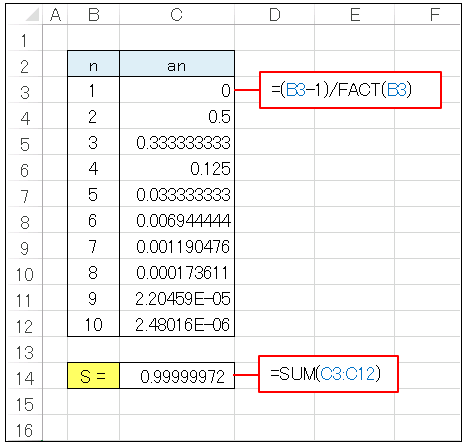
それから数値を合計する SUM関数を使って
=SUM(C3:C12)
と入力すれば求める値が表示されます。最後に計算結果が表示されているセルを右クリックして、[セルの書式設定]、[数値] を順に選択し、小数点以下の桁数を 8 に設定すると 0.99999972 が表示されます。ちなみに級数の式を
\[S=\sum_{k=1}^n\frac{k-1}{k!}=\sum_{k=1}^n\left(\frac{k}{k!}-\frac{1}{k!}\right)=\sum_{k=1}^n\left\{\frac{1}{(k-1)!}-\frac{1}{k!}\right\}\tag{13}\]
と変形して右辺を具体的に書き表してみると最初と最後の項だけが残り、
\[S=\sum_{k=1}^n\frac{k-1}{k!}=1-\frac{1}{n!}\tag{14}\]
となります。つまりある程度 $n$ が大きくなれば、$S\simeq 1$ となるのです。
【VBA】巨大階乗数の計算
ワークシートでは FACT 関数を用いて
=FACT(数値)
とすれば階乗の値を返してくれますが、数値に 171 以上の値を入れるとエラーになってしまいます。エクセルでは 15 桁までの数しか扱えないからです。そこでこの問題を解決するために階乗の値を
\[n!=10^x\tag{15}\]
の形で表すことにして $x$ の部分を求めることにします。
\[n! = n(n – 1)(n – 2)\:\cdots\tag{16}\]
ですから $n$ の 常用対数 をとると
\[\log n!=\log n+\log (n-1)+\log (n -2)+\:\cdots\tag{17}\]
と足し算で表すことができます。まずはこの $\log n!$ を求めるプログラムを作ってみます。
'[VBA] 階乗の対数を計算する関数 Function LOG_FACT(n As Long) As Double Dim k As Long Dim logef As Double If n = 1 Then LOG_FACT = 0 'nが1より大きな整数であれば以下の処理を行う ElseIf n = Int(n) And n > 1 Then 'n!の自然対数を計算します For k = 0 To n - 1 logef = logef + Log(n - k) Next k '常用対数に変換 LOG_FACT = logef / Log(10) Else LOG_FACT = CVErr(xlErrNum) End If End Function
たとえばワークシートのセルに
=LOG_FACT(1000)
と入力すると、「2567.604…」が返ります。これが指数部分 $x$ に相当します。n! の対数値を得ることが目的ならこのままでもいいのですが、あくまで n! の値そのものがほしい場合は別の関数を作って処理する必要があります。 $x$ を整数部分 $a$ と小数部分 $b$ に分けると
\[n!=10^x=10^{\,a+b}=10^{\,b} \times 10^{\,a}\tag{18}\]
のように書くことができます。$10^{\,a}$ はただの桁数です。重要なのは $10^{\,b}$ のところですが、これは小さな値なので問題なく計算できます。桁数 a を取り出すのには TRUNC 関数を使って
=TRUNC(LOG_FACT(数値))
とするだけです。先ほどの例、つまり 1000! の桁数を得るには
=TRUNC(LOG_FACT(1000))
と入力すればよく、結果は 2567 となります(ものすごい桁ですね!)。
POWER_DEC という関数を作って $10^{\,b}$ を計算します。
Function POWERDEC(x As Double) As Double POWER_DEC = 10 ^ (x - Fix(x)) End Function
さきほどの 1000! の例に適用して
=POWER_DEC(LOG_FACT(1000))
とすると 4.0238726 … という値を得ることができます。つまり
\[1000!=4.023873 \times 10^{\,2567}\tag{19}\]
であることがわかりました。

エクセルや数学に関するコメントをお寄せください
二重階乗を階乗で表します。のところで、
(2m−1)!! = 2*m/(2^m*m!) とありますが、これは誤りで、
(2m−1)!! = (2*m)!!/(2*m)! さらに、
= 2^m*m!/(2*m)! ですよね。
御指摘ありがとうございます。
誤記を訂正すると同時に、説明不足な箇所は加筆しておきました。
何しろ一人で書いているので、サイトのあちこちに誤記があると思われます。
今後も誤りを指摘していただけると幸いです。よろしくお願いします。