4進法と10進法・computerの並べ替え

【PS03】4進法と10進法

正の整数を $4$ 進法で表したとき、$1,2,3$ の数字だけを用いて表される数の全体の集合を $M$ とします。$10$ 進法で表したときに $100$ 以上 $200$ 以下になるような $M$ の要素の個数を求めてください。（埼玉大一部改）

【ヒント】とりあえず $100$ と $200$ を $4$ 進法表記に変換してみます。
　
【解答】次のように $100$ と $200$ を $4$ で割っていき、右に余りを書いておきます。



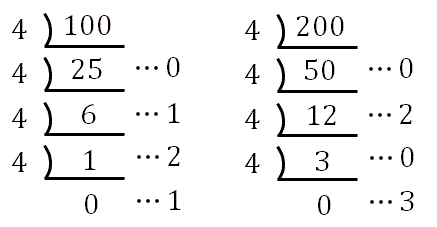
余りを下から拾い上げると、それぞれの $4$ 進法表記が
$$(1210{)}_4,(3020{)}_4$$
であることがわかります（右下の添え字は $4$ 進法であることを示すものです）。いずれも $0$ が含まれているので $M$ の要素ではありませんが、
$$(1210{)}_4+(1{)}_4=(1211{)}_4$$
は $M$ の要素です ($10$ 進法で表すと $101$ です)。また、$3020$ より小さい $M$ の要素は $(2333{)}_4$ です（この数字に $1$ を加えると $(3000{)}_4$ です）。したがって $(1211{)}_4$ 以上、$(2333{)}_4$ 以下で $0$ を含まない数をかぞえればよいことになります。

そこで $M$ の要素を $(abcd{)}_4$ で表して場合分けすると

$a=1,b=2$ のとき、
$c,d$ はそれぞれ $1,2,3$ をとれるので、$3\times 3=9$ 個

$a=1,b=3$ のとき、
$c,d$ はそれぞれ $1,2,3$ をとれるので、$3\times 3=9$ 個

$a=2$ のとき、
$b,c,d$ はそれぞれ $1,2,3$ をとれるので、$3\times 3\times 3=27$ 個

となります。求める個数は合わせて $45$ 個です。

【PS04】computer を並べ替えます

computer に含まれる文字を並び替えて単語を作ります。以下のルールにしたがう並べ方がそれぞれ何通りあるかを答えてください。
(1) 少なくとも一端には子音 c, m, p, t, r のいずれかがくるもの。
(2) 母音 o, u, e の順序を変更しない並べ方。
(3) 母音 3 個と子音 5 個が続いて並んでいるもの。
(4) c と p の間に文字が 2 つあるもの。

【ヒント】順列の基本問題です。(1) は子音が一端、または両端にあるということですから、場合分けで解くと大変面倒です。確率分野の問題で「少なくとも」のような言い回しがあったときには、定番の方法があります。
　
【解答】(1) こういう場合は余事象である「端に子音が１つもないもの」を考えて、全体の順列から引くと簡単に答えが出ます。



上の図にあるように「両端に母音を置く」方法は ${}_3{\mathrm{P}}_2=6$ 通りあって、そのそれぞれの場合に対して、残りの文字の並べ方は $6!$ 通りあるので、余事象の数は
$${}_3{\mathrm{P}}_2\times 6!$$
となります。一方で文字を無条件に並べる方法は $8!$ あるので、求める個数は
$$8!-{}_3{\mathrm{P}}_2\times 6!=(8\cdot 7-6)\times 6!=36000$$
となります。

(2) 条件を満たす順列それぞれについて、母音を並び替えてみることにすると、その方法は $3!=6$ 通りずつあります。たとえば、

computer　o, u, e の並び替え方法は $3!=6$ 通り
cmoputre　o, u, e の並び替え方法は $3!=6$ 通り
ocmpture　o, u, e の並び替え方法は $3!=6$ 通り

というように数えていくと、無条件に並べる順列の数に一致することになります。したがって、求める並べ方の数を $x$ とおくと、
$$6x=8!$$
を満たします。これを解いて $x=6720$ 通りとなります。

(3) 母音 $3$ 個と子音 $5$ 個をそれぞれひとまとめにすると

(oue)(cmptr),　(cmptr)(oue)

の $2$ 通りの配置があって、それぞれの (　) の中の並べ方は $3!$ と $5!$ 通りあるので、答えは
$$2!\times 3!\times 5!=6720$$
となります。

(4) c と p の間に挟まれた文字を (c□□p) のように表すと、$6$ 個の文字から $2$ 文字を選んで □□ の中に並べる方法は
$${}_6{\mathrm{P}}_2=30$$
あります。(c□□p) と残りの $4$ 文字について

(c□□p)□□□□

の並べ方は $5!$ 通りです。さらに c と p を入れ替えることもできるので、答えは
$$30\times 5!\times 2=7200$$
となります。　

【PS05】4項数列の集合

各項が $1,2,3$ のどれかであるような項数 $4$ の数列 $(a_1,a_2,a_3,a_4)$ の集合体を $S$ とします。
(1) $S$ に属する数列は何個ありますか。
(2) $S$ に属する数列で $a_1\le a_2\le a_3\le a_4$ を満たすものは何個ありますか。
(3) $S$ に属する数列で $1,2,3$ のすべてが現れるものは何個ありますか。
(4) $S$ に属する数列で $4$ 項の和が $10$ になるものは何個ありますか。（東大一部改）

【ヒント】
(1) は重複順列（同じものを繰り返しとる順列）です。
(2) は具体的に数え上げるしかありません。
(3) は「どれか 2 つの項は同じである」と考えて分類します。

≫ 同じものを含む順列、重複順列についてはこちらのページを参照してください。
　
【解答】(1) $a_1$ の選び方は $1\sim 3$ のどれでもよいから $3$ 通りです。その各々に対して $a_2$ の選び方も $3$ 通りあります。$a_3,a_4$ についても同じように考えて、$S$ に属する数列の個数は全部で $3^4=81$ 個となります。

(2) １つ１つ丁寧に調べていきます。$a_1=3$ のときは
$$a_2=a_3=a_4=3$$
の $1$ 通りしかありません。$a_1=2$ のときは
$$(a_2,a_3,a_4)=(2,2,2),(2,2,3),(2,3,3),(3,3,3)$$
の $4$ 通りです。$a_1=1$ のときは
$$\begin{array}{rl}(a_2,a_3,a_4)=& (1,1,1),(1,1,2),(1,1,3),(1,2,2),\\ & (1,2,3),(1,3,3),(2,2,2),(2,2,3),\\ & (2,3,3),(3,3,3)\end{array}$$
の $10$ 通りとなります。したがって、題意を満たす数列は合わせて $15$ 個あります。

(3) 数列 $(a_1,a_2,a_3,a_4)$ が $1,2,3$ のすべてをとるということは、必ず同じ数字が $2$ つ含まれているということです。すなわち、それらの数列は
$$\{1,1,2,3\},\{1,2,2,3\},\{1,2,3,3\}$$
の $3$ 組のうちのどれかを並び替えたものとなっているはずです。このうち の１組についての並べ方は $4$ 個の中に同じものを $2$ 個含む順列の数なので、
$${\displaystyle \frac{4!}{2!}=12}$$
となります。よって、題意を満たす数列は全部で $36$ 個あります。

(4) $4$ 個の数字を合計して $10$ になる組合せは
$$\{1,3,3,3\},\{2,2,3,3\}$$
だけです。$\{1,3,3,3\}$ の並べ方は $4$ 個の中に同じものを $3$ 個含む順列、$\{2,2,3,3\}$ の並べ方は $4$ 個の中に同じものを $2$ 個ずつ含む順列なので、題意を満たす数列は
$$\frac{4!}{3!}+\frac{4!}{2!2!}=10$$
となります。