往復バスの遭遇回数

【算数問題51】こばとちゃんと往復バスの遭遇回数

$4.5\,\mathrm{km}$ 離れた A 地点と B 地点をバスが時速 60 km で往復しています。バスが B 地点を出発したのと同時に、こばとちゃんは A 地点から B 地点に向かって時速 $9\,\mathrm{km}$ で移動を始めました。こばとちゃんが B 地点に着くまで何回バスを見かけますか？
 
【ヒント】ダイヤグラムを描く問題です。問題で与えられた単位をメートル (m)、分 (min)、分速 (m/min) に直したほうが解きやすいかもしれません。

【解答】バスとこばとちゃんの速度を分速に直すと
 \[\begin{align*}60[\mathrm{km/h}]&=\frac{60\times 1000[\mathrm{m}]}{60[\mathrm{min}]}=1000[\mathrm{m/min}]\\[6pt]9[\mathrm{km/h}]&=\frac{9\times 1000[\mathrm{m}]}{60[\mathrm{min}]}=150[\mathrm{m/min}]\end{align*}\]
となります。 A 地点と B 地点の距離は $4500\,\mathrm{m}$ ですから、バスが A 地点に達するには
 \[4500[\mathrm{m}]\div 1000[\mathrm{m/min}]=4.5[\mathrm{min}]\]
かかります。つまり往復には $9$ 分かかるということです。また、こばとちゃんは B 地点に到着するまで
 \[4500[\mathrm{m}]\div 150[\mathrm{m/min}]=30[\mathrm{min}]\]
かかります。この状況を図で表してみましょう。
 

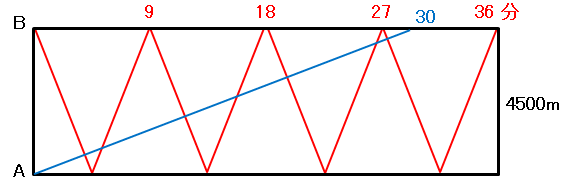
赤い線がバスの移動を、青い線がこばとちゃんの移動を表しています。このような図をダイヤグラムといいます。バスは $9,\,18,\,27,\,36,\,\cdots$ 分に B 地点に戻って来ます。そして $27$ 分を少し過ぎたところでこばとちゃんは B 地点に到着しています。そして赤い線と青い線が交差する点が、お互いが遭遇する位置と時間になっています。交点を数えると $7$ 個ありますから、こばとちゃんは B 地点に着くまで $7$ 回バスを見かけることになります。