正方形の中の正方形（各辺を一定比率で分けます）

【算数問題07】正方形の各辺を 2：1 に分ける点を結んで作る三角形の面積

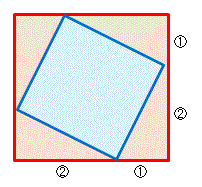(1) 図の赤い正方形の面積は 36 cm² です。この赤い正方形の各辺を 2 ： 1 の比で分ける点を結んで作った青い正方形の面積を求めてください。
　
　
　
　
　

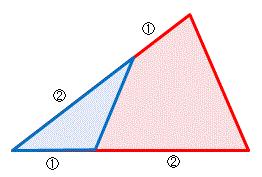
(2) 図の赤い三角形の面積は 36 cm² です。その 2 辺を図のような比率で分けて作った青い三角形の面積を求めてください。
　
　
　
　
【ヒント】(2) は 1 本だけ補助線を引いたほうが見やすくなるかもしれません。三角形の面積は [底辺] × [高さ] ÷ 2 ですから、底辺を分割すると …

【解答】
(1) 大きな赤い正方形の面積は 36 cm² ですから、
　
\[36={6}\times{6}\]
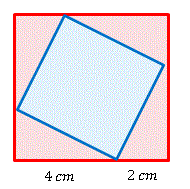
と分解すると 1 辺の長さが 6 cm であることがわかります。その辺を 2 ： 1 の比で分けるのですから、実寸では図のように 4 cm と 2 cm に分けることになりますね。

　すると 青い正方形の面積 を求めるには 赤い正方形の面積 から、底辺が 2 cm, 高さが 4 cm の三角形を 4 つ取りのぞけばよいことになります。

　しかし、2 つの三角形をペアにして長方形 2 つと考えた方が計算が簡単です。縦が 4 cm, 横が 2 cm の長方形の面積は 4 × 2 = 8 cm² ですから、2 つで 16 cm² です。なので、青い正方形の面積は
　
\[36-16=20\ \mathrm{cm}^2\]
となります。

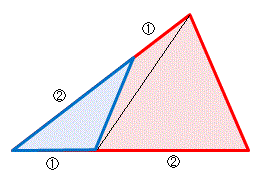(2) 図のように補助線を１本引いておきます。三角形の面積は [底辺] × [高さ] ÷ 2 で求められます。問題では赤い三角形の面積が 36 cm² で与えられています。その底辺を 1 ： 2 で分けると面積もまた 1 ： 2 で分けられることになります。1 ： 2 で分けるということは、1/3 と 2/3 の大きさに分けるということです。補助線によって分けられた左側の三角形の面積は
　
\[36\times\frac{1}{3}=12\ \mathrm{cm}^2\]
となります。この三角形をさらに 2 ： 1 で分けると青い三角形の面積を求めることができますね。青い三角形は分けたうちの大きい方ですから
　
\[12\times\frac{2}{3}=8\ \mathrm{cm}^2\]
が答えとなります。